题目内容
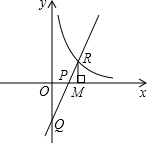 如图,直线y=kx-1(k>0)与双曲线y=
如图,直线y=kx-1(k>0)与双曲线y=| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:先利用直线的解析式求出点Q的坐标,再判定△OPQ与△PRM相似,根据相似三角形面积的比等于相似比的平方求出RM的长度,再根据双曲线的解析式求出点R的坐标,最后把点R的坐标代入直线解析式进行计算即可求出k的值.
解答: 解:设R(m,n),则mn=k.
解:设R(m,n),则mn=k.
∵△OPQ与△PRM的面积是1:4,且△OPQ∽△MPR,
∴OQ:MR=OP:MP=1:2,
令y=kx-1中x=0,解得y=-1,即OQ=1;
令y=0,解得x=
,即OP=
,
∴RM=n=2,
∴OM=3OP,即OM=m=
,
∴R(
,2),
∴mn=
×2=k,
解得:k=±
,
∵k>0,
∴k=
.
故答案为
.
 解:设R(m,n),则mn=k.
解:设R(m,n),则mn=k.∵△OPQ与△PRM的面积是1:4,且△OPQ∽△MPR,
∴OQ:MR=OP:MP=1:2,
令y=kx-1中x=0,解得y=-1,即OQ=1;
令y=0,解得x=
| 1 |
| k |
| 1 |
| k |
∴RM=n=2,
∴OM=3OP,即OM=m=
| 3 |
| k |
∴R(
| 3 |
| k |
∴mn=
| 3 |
| k |
解得:k=±
| 6 |
∵k>0,
∴k=
| 6 |
故答案为
| 6 |
点评:此题考查了一次函数与反比例函数的交点问题,相似三角形的判定与性质,坐标与图形性质,以及函数图象上点的坐标特征,是一道综合性较强的试题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 如图,⊙O与射线AM相切于点B,圆心O在射线AN上,⊙O半径为6cm,OA=10cm.点P从点A出发,以2cm/秒的速度沿AN方向运动,过P点作直线l垂直AB,当l与⊙O相切时,所用时间是( )
如图,⊙O与射线AM相切于点B,圆心O在射线AN上,⊙O半径为6cm,OA=10cm.点P从点A出发,以2cm/秒的速度沿AN方向运动,过P点作直线l垂直AB,当l与⊙O相切时,所用时间是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列说法正确的是( )
| A、直线比射线长 |
| B、过两点有且只有一条直线 |
| C、过三点一定能作出一条直线 |
| D、一个角一定比它的补角小 |
两相似三角形面积之比为1:4,则它们的周长之比为 ( )
| A、1:4 | B、1:16 |
| C、1:2 | D、1:8 |
 如图,△AOB绕点O旋转得到△COD,在这个旋转过程中:
如图,△AOB绕点O旋转得到△COD,在这个旋转过程中: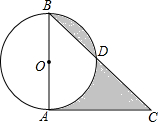 如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则阴影部分的面积为
如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则阴影部分的面积为 如图,在四边形ABCD中,S△ABC=30,S△ACD=15,S△BCD=27,AC与BD交于点O,则S△AOD=
如图,在四边形ABCD中,S△ABC=30,S△ACD=15,S△BCD=27,AC与BD交于点O,则S△AOD=