题目内容
4.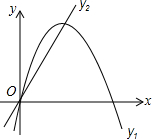 如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的说法有②③.(请填写正确说法的番号)
如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的说法有②③.(请填写正确说法的番号)
分析 若y1=y2,记M=y1=y2.首先求得抛物线与直线的交点坐标,利用图象可得当x>2时,利用函数图象可以得出y2>y1;当0<x<2时,y1>y2;当x<0时,利用函数图象可以得出y2>y1;然后根据当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;即可求得答案.
解答 解:∵当y1=y2时,即-x2+4x=2x时,
解得:x=0或x=2,
∴当x>2时,利用函数图象可以得出y2>y1;当0<x<2时,y1>y2;当x<0时,利用函数图象可以得出y2>y1;
∴①错误;
∵抛物线y1=-x2+4x,直线y2=2x,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;
∴当x<0时,根据函数图象可以得出x值越大,M值越大;
∴②正确;
∵抛物线y1=-x2+4x的最大值为4,故M大于4的x值不存在,
∴③正确;
∵如图:当0<x<2时,y1>y2;
当M=2,2x=2,x=1;
x>2时,y2>y1;
当M=2,-x2+4x=2,x1=2+$\sqrt{2}$,x2=2-$\sqrt{2}$(舍去),
∴使得M=2的x值是1或2+$\sqrt{2}$,
∴④错误;
∴正确的有②③两个.
故答案为②③.
点评 本题考查了二次函数与一次函数综合应用.注意掌握函数增减性是解题关键,注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目
15.下列命题为假命题的是( )
| A. | 在平面内,确定一个物体的位置一般需要两个数据 | |
| B. | 如果两条直线被第三条直线所截,那么内错角相等 | |
| C. | 三角形的一个外角大于任何一个和它不相邻的内角 | |
| D. | 无限不循环小数称为无理数 |
19.在一个不透明的布袋中,红色、黑色的球共有10个,它们除颜色外其他完全相同.张宏通过多次摸球试验后发现其中摸到红球的频率稳定在20%附近,则口袋中红球的个数很可能是( )
| A. | 2个 | B. | 5个 | C. | 8个 | D. | 10个 |
13.下列四幅图中,∠1和∠2是同位角的是( )


| A. | ① | B. | ①② | C. | ①②③ | D. | ①③④ |
 如图,三角形ABC中边AB、AC被直线l所截,图中共有多少对内错角?
如图,三角形ABC中边AB、AC被直线l所截,图中共有多少对内错角? 将一副三角板(△BAC和△ADE)如图放置,若AE∥BC,则∠CAE=30度,∠AFD=75度.
将一副三角板(△BAC和△ADE)如图放置,若AE∥BC,则∠CAE=30度,∠AFD=75度. 如图,阴影部分四边形的两个顶点依次在x轴上,其中横坐标分别为1、3、5的顶点A1、A2、A3在一次函数y=2x+5的图象上,横坐标分别为1、3、5的顶点B1、B2、B3在一次函数y=x+3的图象上,记第一个阴影部分四边形面积为S1,第二个阴影部分四边形面积为S2,第三个阴影部分面积为S3,…,则第2015个阴影部分四边形的面积是( )
如图,阴影部分四边形的两个顶点依次在x轴上,其中横坐标分别为1、3、5的顶点A1、A2、A3在一次函数y=2x+5的图象上,横坐标分别为1、3、5的顶点B1、B2、B3在一次函数y=x+3的图象上,记第一个阴影部分四边形面积为S1,第二个阴影部分四边形面积为S2,第三个阴影部分面积为S3,…,则第2015个阴影部分四边形的面积是( )