题目内容
已知关于x的多项式ax7+bx5+x2+x+12(a、b为常数),且当x=2时,该多项式的值为-8,则当x=-2时,该多项式的值为 .
考点:代数式求值
专题:计算题
分析:把x=2代入多项式得到a×27+b×25+22+2+12=-8,则a×27+b×25=-26,于是当x=-2时,ax7+bx5+x2+x+12=a×(-2)7+b×(-2)5+(-2)2+(-2)+12变形得-(a×27+b×25)+4-2+12,然后把
a×27+b×25=-26整体代入计算即可.
a×27+b×25=-26整体代入计算即可.
解答:解:∵当x=2时,ax7+bx5+x2+x+12=a×27+b×25+22+2+12=-8,
∴a×27+b×25=-26.
当x=-2时,ax7+bx5+x2+x+12=a×(-2)7+b×(-2)5+(-2)2+(-2)+12
=-a×27-b×25+22-2+12
=-(a×27+b×25)+4-2+12
=26+14
=40.
故答案为40.
∴a×27+b×25=-26.
当x=-2时,ax7+bx5+x2+x+12=a×(-2)7+b×(-2)5+(-2)2+(-2)+12
=-a×27-b×25+22-2+12
=-(a×27+b×25)+4-2+12
=26+14
=40.
故答案为40.
点评:本题考查了代数式求值:先根据已知条件得到某代数式的值,然后利用整体的思想求另一个代数式的值.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
 如图为一个几何体的三视图,左视图和主视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的全面积为( )
如图为一个几何体的三视图,左视图和主视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的全面积为( )A、
| ||||
B、12
| ||||
| C、24 | ||||
D、24+2
|
 有一种皮球是由40块黑白相间的牛皮缝制而成的(如图),黑皮可看作五边形,白皮可看作六边形,每块黑皮的周围都是白皮,而每块白皮有三条边和黑皮边在一起,则白皮有( )
有一种皮球是由40块黑白相间的牛皮缝制而成的(如图),黑皮可看作五边形,白皮可看作六边形,每块黑皮的周围都是白皮,而每块白皮有三条边和黑皮边在一起,则白皮有( )| A、16块 | B、20块 |
| C、25块 | D、26块 |
已知一元二次方程x2+mx+3=0配方后为(x+n)2=22,那么一元二次方程x2-mx-3=0配方后为( )
| A、(x+5)2=28 |
| B、(x+5)2=19或(x-5)2=19 |
| C、(x-5)2=19 |
| D、(x+5)2=28或(x-5)2=28 |
 如图,△ABC是等腰直角三角形,AC=BC,D是AC的中点,设∠ABD为α,那么tanα的值为( )
如图,△ABC是等腰直角三角形,AC=BC,D是AC的中点,设∠ABD为α,那么tanα的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
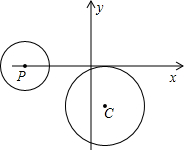 如图,⊙C与x轴相切,点C的坐标为(1,-3).点P在x轴上滑动,当半径为2的⊙P与⊙C外切时,点P的横坐标为
如图,⊙C与x轴相切,点C的坐标为(1,-3).点P在x轴上滑动,当半径为2的⊙P与⊙C外切时,点P的横坐标为