题目内容
 如图,△ABC是等腰直角三角形,AC=BC,D是AC的中点,设∠ABD为α,那么tanα的值为( )
如图,△ABC是等腰直角三角形,AC=BC,D是AC的中点,设∠ABD为α,那么tanα的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:锐角三角函数的定义,等腰直角三角形
专题:常规题型
分析:过点D作DE⊥AB于点E,则△ADE为等腰直角三角形,根据直角三角形斜边等于直角边的
倍表示出AD的长度,再根据中线的定义得到AC,再次利用直角三角形斜边等于直角边的
倍表示出AB的长度,然后求出BE的长度,最后根据正切=
列式计算即可得解.
| 2 |
| 2 |
| 对边 |
| 邻边 |
解答: 解:如图,过点D作DE⊥AB于点E,
解:如图,过点D作DE⊥AB于点E,
∵△ABC是等腰直角三角形,
∴△ADE也是等腰直角三角形,
∴AE=DE,AD=
DE,
∵D是AC的中点,
∴AC=2AD=2
DE,
在等腰直角三角形ABC中,AB=
AC=
×2
DE=4DE,
∴BE=AB-AE=4DE-DE=3DE,
在Rt△BED中,tanα=
=
=
.
故选D.
 解:如图,过点D作DE⊥AB于点E,
解:如图,过点D作DE⊥AB于点E,∵△ABC是等腰直角三角形,
∴△ADE也是等腰直角三角形,
∴AE=DE,AD=
| 2 |
∵D是AC的中点,
∴AC=2AD=2
| 2 |
在等腰直角三角形ABC中,AB=
| 2 |
| 2 |
| 2 |
∴BE=AB-AE=4DE-DE=3DE,
在Rt△BED中,tanα=
| DE |
| BE |
| DE |
| 3DE |
| 1 |
| 3 |
故选D.
点评:本题考查了锐角三角函数的定义,等腰直角三角形的性质,作辅助线构造出以α为内角的直角三角形是解题的关键.

练习册系列答案
相关题目
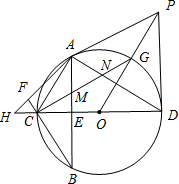 如图,CD为⊙O的直径,弦AB⊥CD于E,OP∥AC,且PD⊥CD,AF⊥BF交DC的延长线于H,连CG,分别交AB、AD于M、N.
如图,CD为⊙O的直径,弦AB⊥CD于E,OP∥AC,且PD⊥CD,AF⊥BF交DC的延长线于H,连CG,分别交AB、AD于M、N.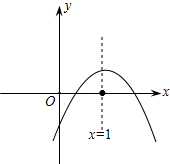 二次函数y=ax2+bx+c的图象如图所示,下列结论:①b>0,②c<0,③b2-4ac>0,④a+b+c>0,⑤4a+2b+c>0.其中正确的有( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:①b>0,②c<0,③b2-4ac>0,④a+b+c>0,⑤4a+2b+c>0.其中正确的有( )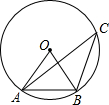 如图,A、B、C三点在⊙O上,∠C=30°,则△OAB是
如图,A、B、C三点在⊙O上,∠C=30°,则△OAB是 直线y=ax+b与y=mx+n位置如图,则方程组
直线y=ax+b与y=mx+n位置如图,则方程组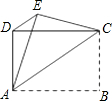 如图,四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,已知DE:AC=5:13,则sin∠CAB=
如图,四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,已知DE:AC=5:13,则sin∠CAB=