题目内容
11．
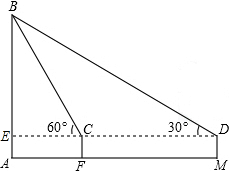如图，小明在M处用高1米（DM=1米）的测角仪测得旗杆AB的顶端B的仰角为30°，再向旗杆方向前进10米到F处，又测得旗杆顶端B的仰角为60°，请求出旗杆AB的高．
分析 求出∠CBD=∠BDE，得到△BCD是等腰三角形，从而求出BC的长，然后在△BEC中，求出BE的长，然后求出AB 的长．
解答 解：∵∠BDE=30°，∠BCE=60°，
∴∠CBD=60°-∠BDE=30°=∠BDE，
∴BC=CD=10米，
在Rt△BCE中，sin∠BCD=$\frac{BE}{BC}$，
即BE=BC•sin60°=10×$\frac{\sqrt{3}}{2}$=5$\sqrt{3}$米，
AB=BE+AE=（5$\sqrt{3}$+1）米．
答：旗杆AB的高度是（5$\sqrt{3}$+1）米．
点评 本题考查了解直角三角形的应用-仰角俯角问题，会解直角三角形是解题的关键．
练习册系列答案
相关题目
观察图形由（1）→（2）的变化过程，写出A、B对应点的坐标分别为（2，-3），（4，-1）．