题目内容
4．已知x3-2x-4=0，求-2x3-x2+18x的值．分析 根据x3-2x-4=0得到x3-2x2+2x2-4x+2x-4=0，提取公因式后得到（x2+2x+2）（x-2）=0，根据x2+2x+2=（x+1）2+1＞0，得到x-2=0，从而求得x的值，代入代数式即可求值．
解答 解：∵x3-2x-4=0，
∴x3-2x2+2x2-4x+2x-4=0，
∴x2（x-2）+2x（x-2）+2（x-2）=0，
∴（x2+2x+2）（x-2）=0，
∵x2+2x+2=（x+1）2+1＞0，
∴x-2=0，
∴x=2，
将x=2代入得原式=-2×23-22-18×2
=-16-4+36
=16．
点评 本题考查了因式分解的应用，将已知条件变形后提取公因式后利用非负数的性质即可求得x的值，代入即可求解．
练习册系列答案
相关题目
14．观察下列图形中点的个数，根据其中蕴含的规律回答下列问题：
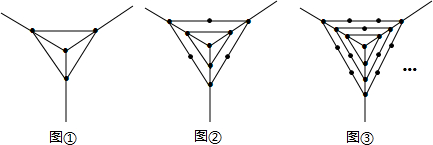
（1）填写下表：
（2）用代数式表示第n个图形中点的个数$\frac{3}{2}$n（n+1）+1个．
（1）填写下表：
| 图形编号 | ① | ② | ③ | … |
| 图形中点的个数 | 4 | 10 | 19 |
如图所示，△ABC为等边三角形，DB=DE，∠BDE=120°，F为CE的中点，求证：AF⊥DF．
如图，能通过图形的旋转，使图形A与图形B重合吗？如果用两种图形的运动呢？比如旋转和轴对称，旋转和平移等．用扑克牌试一试，说出一种方法．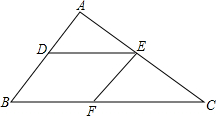
如图，在△ABC中，D，E，F分别是AB，AC，BC上的点，且DE∥BC，EF∥AB，$\frac{AD}{BD}$=$\frac{2}{3}$，BC=40，求CF的长．
16．在a，b，c，d，e中有3个负数，则abcde的积（ ）
| A． | 大于0 | B． | 小于0 | C． | 大于或等于0 | D． | 小于或等于0 |
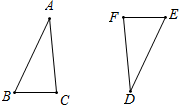如图，△ABC和△DEF关于点O成心对称．
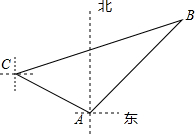如图，我国海上休渔结束后，甲、乙两艘捕鱼船分别从相距30$\sqrt{2}$千米的A港、C港出海捕鱼，C港在A港北偏西60°处，甲船以每小时15千米的速度沿东北方向航行，甲船航行2小时后乙船快速（匀速）沿北偏东75°的方向航行，结果两船在B处相遇．