题目内容
9．
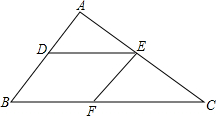如图，在△ABC中，D，E，F分别是AB，AC，BC上的点，且DE∥BC，EF∥AB，$\frac{AD}{BD}$=$\frac{2}{3}$，BC=40，求CF的长．
分析 根据平行线分线段成比例定理求出$\frac{DE}{BC}$=$\frac{2}{5}$，求出DE的长，根据平行四边形的性质得到BF=DE，得到答案．
解答 解：∵DE∥BC，
∴$\frac{DE}{BC}$=$\frac{AD}{AB}$=$\frac{2}{5}$，又BC=40，
∴DE=16，
∵DE∥BC，EF∥AB，
∴四边形DBFE是平行四边形，
∴BF=DE=16，
∴CF=BC-BF=24．
点评 本题考查的是平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键．
练习册系列答案
相关题目
如图，已知△ABC≌△FED，且BC=ED，那么AB与EF平行吗？为什么？
如图，放牛娃准备从家（点A处）牵牛到草地边（OP边）吃草，然后到河边（OQ边）饮水最后返回家中，（∠POQ＜90°），请你帮他设计一条最短的行走路线，并在图①中画出．