题目内容
14.观察下列图形中点的个数,根据其中蕴含的规律回答下列问题: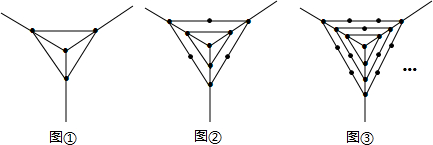
(1)填写下表:
| 图形编号 | ① | ② | ③ | … |
| 图形中点的个数 | 4 | 10 | 19 |
分析 (1)图①点的个数为1+3=4,图②点的个数为1+3+6=10,图③点的个数为1+3+6+9=9,…由此得出图n点的个数为1+1×3+2×3+3×3+…+3n=$\frac{3}{2}$n(n+1)+1,由此规律得出答案即可;
(2)利用(1)中的规律得出答案即可.
解答 解:(1)填写下表:
| 图形编号 | ① | ② | ③ | … |
| 图形中点的个数 | 4 | 10 | 19 |
故答案为:4,10,19;$\frac{3}{2}$n(n+1)+1.
点评 此题考查图形的变化规律,找出图形之间的联系,得出运算规律,利用规律解决问题.

练习册系列答案
相关题目
4.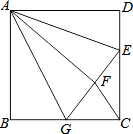 如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:
如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:
①点G是BC中点;②FG=FC;③EF=FC;④∠GAE=45°;⑤S△FGC=$\frac{9}{10}$.
其中正确的有( )
 如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:
如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:①点G是BC中点;②FG=FC;③EF=FC;④∠GAE=45°;⑤S△FGC=$\frac{9}{10}$.
其中正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.中国现行的个人所得税法自2011年9月1日起施行,其中规定个人所得税纳税办法如下:
一.以个人每月工资收入额减去3500元后的余额作为其每月应纳税所得额;
二.个人所得税纳税税率如表所示:
(1)若甲、乙两人的每月工资收入额分别为4000元和6000元,请分别求出甲、乙两人的每月应缴纳的个人所得税;
(2)若丙每月收入为x元,且8000<x<12500,写出丙每月缴纳的个人所得税y(元)与x的函数关系式.
一.以个人每月工资收入额减去3500元后的余额作为其每月应纳税所得额;
二.个人所得税纳税税率如表所示:
| 纳税级数 | 个人每月应纳税所得额 | 税率 |
| 1 | 不超过1500元的部分 | 3% |
| 2 | 超过1500元至4500元的部分 | 10% |
| 3 | 超过4500元至9000元的部分 | 20% |
| 4 | 超过9000元至35000元的部分 | 25% |
| 5 | 超过35000元至55000元的部分 | 30% |
| 6 | 超过55000元至80000元的部分 | 35% |
| 7 | 超过80000元的部分 | 45% |
(2)若丙每月收入为x元,且8000<x<12500,写出丙每月缴纳的个人所得税y(元)与x的函数关系式.
3.已知A,B,C,D都是⊙O上的点,则下列命题中不一定为真命题的是( )
| A. | 如果∠AOB=∠COD,那么$\widehat{AB}$=$\widehat{CD}$ | B. | 如果$\widehat{AB}$=$\widehat{CD}$,那么∠AOB=∠COD | ||
| C. | 如果$\widehat{AB}$=$\widehat{CD}$,那么AB=CD | D. | 如果AB=CD,那么$\widehat{AB}$=$\widehat{CD}$ |
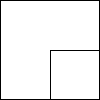 如图是一幅“斜阳正方形”,最大正方形的边长为a米,第二个正方形的边长是$\frac{a}{2}$米,第三个正方形的边长是$\frac{a}{4}$米,…以此类推.
如图是一幅“斜阳正方形”,最大正方形的边长为a米,第二个正方形的边长是$\frac{a}{2}$米,第三个正方形的边长是$\frac{a}{4}$米,…以此类推. 如图所示,在公路MN的北侧有A、B两家工厂,现要在公路边建一仓库P,要求路程PA与PB的和最短,请用所学的知识确定点P的位置.
如图所示,在公路MN的北侧有A、B两家工厂,现要在公路边建一仓库P,要求路程PA与PB的和最短,请用所学的知识确定点P的位置. 如图,已知△ABC≌△FED,且BC=ED,那么AB与EF平行吗?为什么?
如图,已知△ABC≌△FED,且BC=ED,那么AB与EF平行吗?为什么?