题目内容
11.若实数a、b、c满足$\sqrt{b-2a+3}$+|a+b|=$\sqrt{c-4}$+$\sqrt{4-c}$,则2a-3b+c2的值为21.分析 首先根据二次根式有意义的条件可确定c=4,再根据非负数的性质可得$\left\{\begin{array}{l}{b-2a+3=0}\\{a+b=0}\end{array}\right.$,解方程组可得答案.
解答 解:由题意得:$\left\{\begin{array}{l}{c-4≥0}\\{4-c≥0}\end{array}\right.$,
解得:c=4,
∵$\sqrt{b-2a+3}$+|a+b|=$\sqrt{c-4}$+$\sqrt{4-c}$,
∴$\sqrt{b-2a+3}$+|a+b|=0,
∴$\left\{\begin{array}{l}{b-2a+3=0}\\{a+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-1}\end{array}\right.$,
∴2a-3b+c2=2+3+16=21,
故答案为:21.
点评 此题主要考查了二次根式有意义和非负数的性质,关键是掌握二次根式中的被开方数是非负数.

练习册系列答案
相关题目
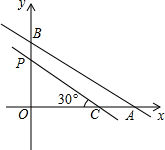 如图,在直角坐标系中,一次函数在y轴上的交点坐标是B(0,5),与x轴交于点A的横坐标是图象与y轴交点到原点距离的2倍,点C的坐标是(6,0),点P的坐标是(0,y)
如图,在直角坐标系中,一次函数在y轴上的交点坐标是B(0,5),与x轴交于点A的横坐标是图象与y轴交点到原点距离的2倍,点C的坐标是(6,0),点P的坐标是(0,y) 如图,小明在打网球时,使球恰好能打过网,而且落在离网4米的位置上,求球拍击球的高度h=1.125米.
如图,小明在打网球时,使球恰好能打过网,而且落在离网4米的位置上,求球拍击球的高度h=1.125米.