题目内容

20．将抛物线y=-x2+2x+3在x轴上方的部分沿x轴翻折至x轴下方，图象的剩余部分不变，得到一个新的函数图象，那么直线y=x+b与此新图象的交点个数的情况有（　　）种．
A．6B．5C．4D．3

分析 首先根据题意画出函数图象，然后平移直线y=k+b，找出两函数图象的交点个数即可．

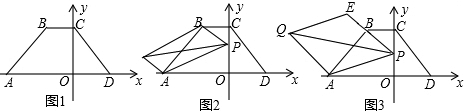
解答 解：如图1，所示：函数图象没有交点．

如图2所示：函数图象有1个交点．

如图3所示，图象有两个交点．

如图4所示函数图象有3个交点．

如图5所示，图象有4个交点．

综上所述，共有5种情况．
故选：B．

点评 本题主要考查的是二次函数图象与一次函数图象的交点问题，根据题意画出函数图象是解答此类问题的常用方法．

练习册系列答案
相关题目
10．将7写成一个正数的平方形式为：7=（$\sqrt{7}$）2．
11．若实数a、b、c满足$\sqrt{b-2a+3}$+|a+b|=$\sqrt{c-4}$+$\sqrt{4-c}$，则2a-3b+c2的值为21．
8．以下方程中，一定是关于x的一元二次方程的是（　　）
A．ax2+bx+c=0B．2x2+3x=2x（x-1）C．（k2+1）x2-2x=6D．x2-$\frac{5}{x}$+1=0
15．为了考察一批电视机的使用寿命，从中任意抽取了10台进行实验，在这个问题中样本是（　　）
A．抽取的10台电视机B．这一批电视机的使用寿命
C．10D．抽取的10台电视机的使用寿命
5．计算：2-1+tan45°-|2-$\root{3}{27}$|+$\sqrt{18}$÷$\sqrt{8}$．
2．如图1，等腰梯形ABCD，AB=CD，BC∥AD，BC⊥y轴，C为垂足．点A（-3，0），B（-1，2）．
（1）直接写出点C、D的坐标．C（0，2），D（2，0）．
（2）如图2，若P为线段OC上一点，连接PA、PB，以PA、PB为边作平行四边形PAQB，连接PQ，交AB于点G．试探究：
①是否存在这样的点P，使对角线PQ，AB的长相等，为什么？
②是否存在这样的点P，使得PQ取得最小值？若存在，请求出这个最小值，并求出此时点P的坐标；若不存在，请说明理由．
（3）如图3，P为线段OC上任意一点，延长PB到E，使BE=PB，以PE、PA为边作平行四边形PAQE，连接PQ．请探究对角线PQ的长是否也存在最小值？如果存在，直接写出最小值；如果不存在，请说明理由．
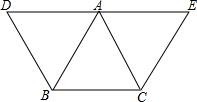19．如图所示，已知BD∥AC，CE∥BA，且点D、A、E在一条直线上，设∠BAC=x，∠D+∠E=y．
（1）试用x的式子表示y；
（2）当x=90°时，判断直线DB与直线EC的位置关系，并说明理由．
20．下列去括号正确的是（　　）
A．+（x-6）=-x+6B．-（x-6）=x+6C．-（x-6）=x-6D．-（x-6）=-x+6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网