题目内容
6．
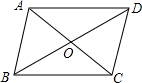平行四边形ABCD中，AC、BD交于O点，下列条件中，能使四边形ABCD是矩形的是（ ）| A． | AC⊥BD | B． | AO=BO | C． | AB=AD | D． | AO=CO |
分析 根据矩形的判定定理对角线互相平分且相等的四边形是矩形，以及利用菱形的判定定理分别得出图形的形状，据此分析判断．
解答 解：A．AC⊥BD，对角线互相垂直，可判定平行四边形ABCD是菱形．故此选项错误；
B、∵AO=BO，∴AC=BD，可判定平行四边形ABCD是矩形，此选项正确；
C、邻边相等能判定得到菱形，故此选项错误；
D．平行四边形的对角线互相平分．故此选项错误．
故选：B．
点评 此题主要考查了矩形的判定，此题用到的知识点为：对角线相等的平行四边形是矩形，注意与菱形的判定比较有利于对知识的灵活应用．
练习册系列答案
阅读快车系列答案
相关题目
16．如果a＜b，下列各式中不一定正确的是（ ）
| A． | a-1＜b-1 | B． | $\frac{1}{a}$＜$\frac{1}{b}$ | C． | -3a＞-3b | D． | $\frac{a}{4}$＜$\frac{b}{4}$ |
17．过A（-5，-4）和B（-5，4）两点的直线一定（ ）
| A． | 垂直于x轴 | B． | 与x轴相交但不平行于x轴 | ||
| C． | 平行于x轴 | D． | 与x轴、y轴都不平行 |
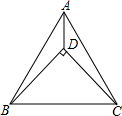如图，等腰直角三角形BDC的顶点D在等边三角形ABC的内部，∠BDC=90°，连接AD，过点D作一条直线将△ABD分割成两个等腰三角形，则分割出的这两个等腰三角形的顶角分别是120，150度．
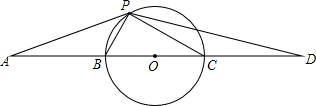如图，点B，C是线段AD的三等分点，以BC为直径作⊙O，点P是圆上异于B，C的任意一点，连接PA，PB，PC，PD．
11．在Rt△ABC中，已知两边长分别是3和4，则第三边长为（ ）
| A． | 5 | B． | $\sqrt{7}$ | C． | 5或$\sqrt{7}$ | D． | 无法确定 |
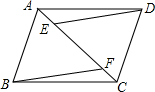如图，已知四边形ABCD中，连接AC，点E、F在AC上，AE=CF，连接DE，BF，且DE$\underset{∥}{=}$BF，求证：四边形ABCD是平行四边形．