题目内容
 如图,在抛物线y=x2上取一点P,在x轴上取一点A,使OP=PA,过点A作x轴的垂线与直线OP交于点Q,当△APQ为正三角形时,试求△APQ的面积.
如图,在抛物线y=x2上取一点P,在x轴上取一点A,使OP=PA,过点A作x轴的垂线与直线OP交于点Q,当△APQ为正三角形时,试求△APQ的面积.考点:二次函数图象上点的坐标特征
专题:计算题
分析:作PH⊥OA于H,如图,根据二次函数图象上点的坐标特征可设P(t,t2),由PA=PO得到OA=OH,∠POA=∠PAO,再利用△APQ为正三角形得到PQ=PA,∠APQ=60°,所以PO=PQ,∠POA=30°,然后在Rt△POH中,根据含30度的直角三角形三边的关系得t=
t2,解得t1=
,t2=0(舍去),即OH=
,PH=
,
所以OA=2OH=
,然后根据S△PAQ=S△POA和三角形面积公式计算.
| 3 |
| ||
| 3 |
| ||
| 3 |
| 1 |
| 3 |
所以OA=2OH=
2
| ||
| 3 |
解答:解:作PH⊥OA于H,如图,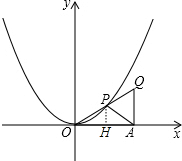 设P(t,t2),
设P(t,t2),
∵PA=PO,
∴OA=OH,∠POA=∠PAO,
∵△APQ为正三角形,
∴PQ=PA,∠APQ=60°,
∴PO=PQ,∠POA=30°,
在Rt△POH中,∵∠POH=30°,OH=t,PH=t2,
∴OH=
PH,即t=
t2,解得t1=
,t2=0(舍去),
∴OH=
,PH=
,
∴OA=2OH=
,
∵OP=PQ,
∴S△PAQ=S△POA=
•
•
=
.
 设P(t,t2),
设P(t,t2),∵PA=PO,
∴OA=OH,∠POA=∠PAO,
∵△APQ为正三角形,
∴PQ=PA,∠APQ=60°,
∴PO=PQ,∠POA=30°,
在Rt△POH中,∵∠POH=30°,OH=t,PH=t2,
∴OH=
| 3 |
| 3 |
| ||
| 3 |
∴OH=
| ||
| 3 |
| 1 |
| 3 |
∴OA=2OH=
2
| ||
| 3 |
∵OP=PQ,
∴S△PAQ=S△POA=
| 1 |
| 2 |
2
| ||
| 3 |
| 1 |
| 3 |
| ||
| 9 |
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了等边三角形的性质.

练习册系列答案
相关题目
 如图,直线AB与y轴、x轴交点分别为A(0,2)、B(4,0),求直线AB的解析式及△AOB的面积.
如图,直线AB与y轴、x轴交点分别为A(0,2)、B(4,0),求直线AB的解析式及△AOB的面积.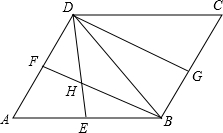 如图,在?ABCD中,∠A=60°,∠ABD、∠ADB、∠CDB的平分线分别为BF、DE、DG,与?ABCD的边分别交于点F、E、G.
如图,在?ABCD中,∠A=60°,∠ABD、∠ADB、∠CDB的平分线分别为BF、DE、DG,与?ABCD的边分别交于点F、E、G.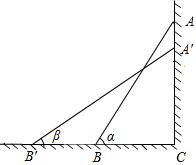 如图,AB是斜靠在墙上的长梯,AB与地面的夹角为α,当梯顶A下滑1m至A′时,梯脚B滑至B′,A′B′与地面的夹角为β,若tanα=
如图,AB是斜靠在墙上的长梯,AB与地面的夹角为α,当梯顶A下滑1m至A′时,梯脚B滑至B′,A′B′与地面的夹角为β,若tanα=