题目内容
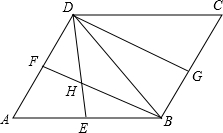 如图,在?ABCD中,∠A=60°,∠ABD、∠ADB、∠CDB的平分线分别为BF、DE、DG,与?ABCD的边分别交于点F、E、G.
如图,在?ABCD中,∠A=60°,∠ABD、∠ADB、∠CDB的平分线分别为BF、DE、DG,与?ABCD的边分别交于点F、E、G.试说明:(1)DF=BG;
(2)BE+BG=BD.
考点:平行四边形的性质,全等三角形的判定与性质
专题:证明题
分析:(1)由四边形ABCD是平行四边形,可得AB∥CD,AD∥BC,又由∠ABD、∠CDB的平分线分别为BF、DG,易证得∠FBD=∠GDB,即可证得DG∥BF,则可证得四边形DFBG是平行四边形,继而证得结论;
(2)首先在BD截取BM=BE,连接HM,易证得△BEH≌△BMH,继而证得△DFH≌△DMH,则可证得结论.
(2)首先在BD截取BM=BE,连接HM,易证得△BEH≌△BMH,继而证得△DFH≌△DMH,则可证得结论.
解答:证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,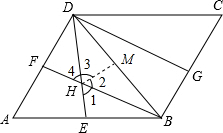
∴∠ABD=∠CDB,
∵∠ABD、∠CDB的平分线分别为BF、DG,
∴∠FBD=
∠ABD,∠GDB=
∠CDB,
∴∠FBD=∠GDB,
∴DG∥BF,
∴四边形DFBG是平行四边形,
∴DF=BG;
(2)在BD截取BM=BE,连接HM,
∵∠A=60°,∠ABD、∠ADB的平分线分别为BF、DE,
∴∠1=∠4=60°,∠BHD=120°,
在△BEH和△BMH中,
,
∴△BEH≌△BMH(SAS),
∴∠1=∠2=∠3=∠4=60°,
在△DFH和△DMH中,
,
∴△DFH≌△DMH(ASA),
∴DF=DM,
∴BD=BM+DM=BE+DF=BE+BG.
∴AB∥CD,AD∥BC,

∴∠ABD=∠CDB,
∵∠ABD、∠CDB的平分线分别为BF、DG,
∴∠FBD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠FBD=∠GDB,
∴DG∥BF,
∴四边形DFBG是平行四边形,
∴DF=BG;
(2)在BD截取BM=BE,连接HM,
∵∠A=60°,∠ABD、∠ADB的平分线分别为BF、DE,
∴∠1=∠4=60°,∠BHD=120°,
在△BEH和△BMH中,
|
∴△BEH≌△BMH(SAS),
∴∠1=∠2=∠3=∠4=60°,
在△DFH和△DMH中,
|
∴△DFH≌△DMH(ASA),
∴DF=DM,
∴BD=BM+DM=BE+DF=BE+BG.
点评:此题考查了平行四边形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知抛物线y=x2-x-1与x轴的一个交点为(m,0),则代数m2-m+100的值为( )
| A、98 | B、109 |
| C、99 | D、101 |
 如图,在抛物线y=x2上取一点P,在x轴上取一点A,使OP=PA,过点A作x轴的垂线与直线OP交于点Q,当△APQ为正三角形时,试求△APQ的面积.
如图,在抛物线y=x2上取一点P,在x轴上取一点A,使OP=PA,过点A作x轴的垂线与直线OP交于点Q,当△APQ为正三角形时,试求△APQ的面积. 如图,A、B、C、D是圆上的四点,AC=BD,求证:AD∥BC.
如图,A、B、C、D是圆上的四点,AC=BD,求证:AD∥BC.