题目内容
13. 如图,∠AOC和∠BOD都是直角.如果∠DOC=28°,则下列判断错误的是( )
如图,∠AOC和∠BOD都是直角.如果∠DOC=28°,则下列判断错误的是( )| A. | ∠AOD=∠BOC | B. | ∠AOB=148° | ||
| C. | ∠AOB+∠DOC=180° | D. | 若∠DOC变小,则∠AOB变大 |
分析 A、根据同角的余角相等即可求解;
B、先根据余角的定义求出∠AOD,再根据角的和差关系即可求解;
C、根据角的和差关系即可求解;
D、根据∠AOD+∠DOC+∠DOC+∠BOC=180°,可得∠AOB+∠DOC=180°,进而得到∠DOC变小∠AOB变大.
解答 解:A、∵∠AOC和∠BOD都是直角,
∴∠AOD+∠DOC=∠DOC+∠BOC=90°,
∴∠AOD=∠BOC,故A正确,不符合题意;
B、∵∠DOC=28°,
∴∠AOD=62°,
∴∠AOB=62°+90°=152°,故B错误,符合题意,
C、∵∠AOD+∠DOC=∠DOC+∠BOC=90°,
∴∠AOD+∠DOC+∠DOC+∠BOC=180°,
∴∠AOB+∠DOC=180°,故C正确,不符合题意;
D、∵∠AOD+∠DOC+∠DOC+∠BOC=180°,
∴∠AOB+∠DOC=180°,
∴∠DOC变小,则∠AOB变大.
故选:B.
点评 本题考查了余角和补角,以及角的计算,是基础题,准确识图是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.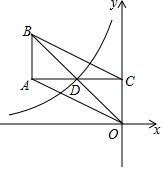 如图,双曲线y=-$\frac{3}{2x}$(x<0)经过?ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则?OABC的面积是( )
如图,双曲线y=-$\frac{3}{2x}$(x<0)经过?ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则?OABC的面积是( )
 如图,双曲线y=-$\frac{3}{2x}$(x<0)经过?ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则?OABC的面积是( )
如图,双曲线y=-$\frac{3}{2x}$(x<0)经过?ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则?OABC的面积是( )| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | 3 | D. | 6 |
2. 如图,在?ABCD中,对角线AC、BD相交于点O,则下列式子不正确的是( )
如图,在?ABCD中,对角线AC、BD相交于点O,则下列式子不正确的是( )
 如图,在?ABCD中,对角线AC、BD相交于点O,则下列式子不正确的是( )
如图,在?ABCD中,对角线AC、BD相交于点O,则下列式子不正确的是( )| A. | BO=OD | B. | AB=CD | C. | ∠BAD=∠BCD | D. | AC=BD |
18. 下面是一组同学做“抛掷质地均匀的硬币试验”获得的数据.
下面是一组同学做“抛掷质地均匀的硬币试验”获得的数据.
(1)填写表中的空格;
(2)画出折线统计图;
(3)抛掷质地均匀的硬币,正面朝上的概率的估计值是多少?
 下面是一组同学做“抛掷质地均匀的硬币试验”获得的数据.
下面是一组同学做“抛掷质地均匀的硬币试验”获得的数据.| 抛掷次数 | 100 | 200 | 300 | 400 | 500 |
| 正面朝上的 频数m | 51 | 98 | 153 | 200 | 250 |
| 正面朝上的 频率mn | 0.51 | 0.49 | 0.51 | 0.50 | 0.51 |
(2)画出折线统计图;
(3)抛掷质地均匀的硬币,正面朝上的概率的估计值是多少?
2.$\sqrt{3}$•$\sqrt{\frac{6}{x}}$是整数,那么x是( )
| A. | 6和3 | B. | 3和1 | C. | 2和18 | D. | 只有18 |
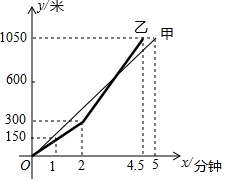 百舸竞渡,激情飞扬.端午节期间,某地举行龙舟比赛.甲、乙两支龙舟队在比赛时路程y(米)与时间x(分钟)之间的函数图象如图所示.根据图象回答下列问题:
百舸竞渡,激情飞扬.端午节期间,某地举行龙舟比赛.甲、乙两支龙舟队在比赛时路程y(米)与时间x(分钟)之间的函数图象如图所示.根据图象回答下列问题: