题目内容
10.解方程(1)2x2-4x-10=0 (用配方法)
(2)2x2+3x=4(公式法)
(3)(x-2)2=2(x-2)
(4)x2-4x-5=0.
分析 (1)方程利用配方法求出解即可;
(2)方程利用公式法求出解即可;
(3)方程移项后,利用因式分解法求出解即可;
(4)方程利用因式分解法求出解即可.
解答 解:(1)方程变形得:x2-2x=5,
配方得:x2-2x+1=6,即(x-1)2=6,
开方得:x-1=±$\sqrt{6}$,
解得:x1=1+$\sqrt{6}$,x2=1-$\sqrt{6}$;
(2)方程整理得:2x2+3x-4=0,
这里a=2,b=3,c=-4,
∵△=9+32=41,
∴x=$\frac{-3±\sqrt{41}}{4}$;
(3)方程移项得(x-2)2-2(x-2)=0,
分解因式得:(x-2)(x-4)=0,
解得:x1=2,x2=4;
(4)分解因式得:(x-5)(x+1)=0,
可得x-5=0或x+1=0,
解得:x1=5,x2=-1.
点评 此题考查了解一元二次方程-因式分解法,公式法,以及直接开平方法,熟练掌握各种解法是解本题的关键.

练习册系列答案
相关题目
5.已知xm=a,xn=b,那么xm+2n的值等于( )
| A. | a+2b | B. | a+b2 | C. | ab2 | D. | amb2n |
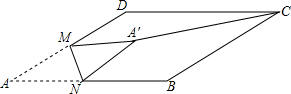 如图,在平行四边形ABCD中,∠BCD=30°,BC=4,CD=3$\sqrt{3}$,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是5.
如图,在平行四边形ABCD中,∠BCD=30°,BC=4,CD=3$\sqrt{3}$,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是5.