题目内容
6.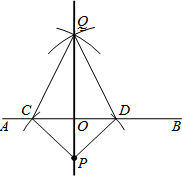 我们知道,用直尺和圆规经过直线AB外一点P作直线AB的垂线的方法如下:
我们知道,用直尺和圆规经过直线AB外一点P作直线AB的垂线的方法如下:| 作 法 | 图 形 |
| (1)以点P为圆心,适当的长为半径作弧,使它与AB交于点C、D; (2)分别以C、D为圆心,大于$\frac{1}{2}$CD的长为半径作弧,两弧交于点Q; (3)作直线PQ. 直线PQ就是所求的垂线. | 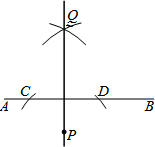 |
分析 根据作图可得CQ=DQ,CP=DP,再根据垂直平分线的判定可得Q、P都在CD的垂直平分线上,根据两点确定一条直线可得PQ⊥AB.
解答 解:∵CQ=DQ,
∴Q在CD的垂直平分线上,
∵CP=DP,
∴P在CD的垂直平分线上,
∴QP是CD的垂直平分线,
∴PQ⊥AB.
点评 此题主要考查了基本作图,关键是掌握到线段两端点距离相等的点在线段的垂直平分线上.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
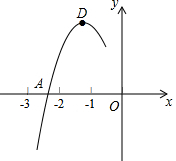 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论: