题目内容
14.一个多边形的每一个外角都相等,一个内角和一个外角之比为9:2,求这个多边形的边数.分析 先根据多边形的内角和外角的关系,求出一个外角.再根据外角和是固定的360°,从而可代入公式求解.
解答 解:设多边形的一个内角为9x度,则一个外角为2x度,依题意得
9x+2x=180°
解得x=($\frac{180}{11}$)°
360°÷[2×($\frac{180}{11}$)°]=11.
答:这个多边形的边数为11.
点评 本题考查多边形的内角与外角关系、方程的思想.关键是记住多边形的一个内角与外角互补、及外角和的特征.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
5.在-2,π,2x,x+1,$\frac{xy}{2}$中,代数式有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.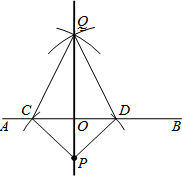 我们知道,用直尺和圆规经过直线AB外一点P作直线AB的垂线的方法如下:
我们知道,用直尺和圆规经过直线AB外一点P作直线AB的垂线的方法如下:
若连接CP、DP、CQ、DQ,直线AB、PQ的交点为O,你能利用“已学的数学知识”来证明PQ⊥AB吗?若能,请写出证明过程;若不能,请说明理由.
 我们知道,用直尺和圆规经过直线AB外一点P作直线AB的垂线的方法如下:
我们知道,用直尺和圆规经过直线AB外一点P作直线AB的垂线的方法如下:| 作 法 | 图 形 |
| (1)以点P为圆心,适当的长为半径作弧,使它与AB交于点C、D; (2)分别以C、D为圆心,大于$\frac{1}{2}$CD的长为半径作弧,两弧交于点Q; (3)作直线PQ. 直线PQ就是所求的垂线. | 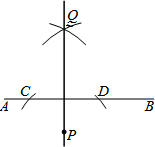 |
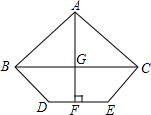 如图,AB=AC,BC∥DE,AF垂直平分DE,求证:BD=CE.
如图,AB=AC,BC∥DE,AF垂直平分DE,求证:BD=CE.