题目内容
18.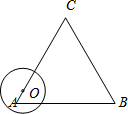 如图,动点O从边长为6的等边△ABC的顶点A出发,沿着A→C→B→A的路线匀速运动一周,速度为1个单位长度每秒.以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第三次相切时是点O出发后第( )秒.
如图,动点O从边长为6的等边△ABC的顶点A出发,沿着A→C→B→A的路线匀速运动一周,速度为1个单位长度每秒.以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第三次相切时是点O出发后第( )秒.| A. | 2 | B. | 4 | C. | 8 | D. | 10 |
分析 若以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第三次相切,即为当点O在BC上,且和AC边相切的情况.作O′D⊥AC于D,则O′D=$\sqrt{3}$,利用解直角三角形的知识,进一步求得O′C=2,由此即可解决问题.
解答 解:根据题意,则作O′D⊥AC于D,则O′D=$\sqrt{3}$,
在Rt△O′CD中,∠C=60°,O′D=$\sqrt{3}$,
∴O′C=2,
∴点O运动的路程为6+2=8,
∴t=$\frac{8}{1}$=8
∴以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第三次相切时是出发后第8秒.
故选C.
点评 此题考查了直线和圆相切时数量之间的关系,解题的关键是能够正确分析出以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第三次相切时的位置.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
20.计算:$\sqrt{32}-\sqrt{8}$的结果是( )
| A. | $\sqrt{24}$ | B. | $2\sqrt{6}$ | C. | $3\sqrt{2}$ | D. | $2\sqrt{2}$ |
6.已知:A(3,4),将OA绕原点O逆时针旋转90°得到OA′,则点A′的坐标是( )
| A. | (-3,4) | B. | (-4,3) | C. | (3,-4) | D. | (4,-3) |
13.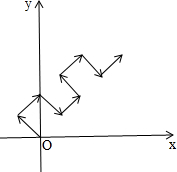 一个质点从原点开始在x轴上方按如图中箭头所示方向运动且每次运动相同的距离,第1次,它从原点运动到(-1,1),第2次从(-1,1)运动到(0,2),…,即:(0,0)→(-1,1)→(0,2)→(1,1)→(2,2)→(1,3)→(2,4)→(3,3)→…,那么质点第20次移动到达的位置的坐标是( )
一个质点从原点开始在x轴上方按如图中箭头所示方向运动且每次运动相同的距离,第1次,它从原点运动到(-1,1),第2次从(-1,1)运动到(0,2),…,即:(0,0)→(-1,1)→(0,2)→(1,1)→(2,2)→(1,3)→(2,4)→(3,3)→…,那么质点第20次移动到达的位置的坐标是( )
 一个质点从原点开始在x轴上方按如图中箭头所示方向运动且每次运动相同的距离,第1次,它从原点运动到(-1,1),第2次从(-1,1)运动到(0,2),…,即:(0,0)→(-1,1)→(0,2)→(1,1)→(2,2)→(1,3)→(2,4)→(3,3)→…,那么质点第20次移动到达的位置的坐标是( )
一个质点从原点开始在x轴上方按如图中箭头所示方向运动且每次运动相同的距离,第1次,它从原点运动到(-1,1),第2次从(-1,1)运动到(0,2),…,即:(0,0)→(-1,1)→(0,2)→(1,1)→(2,2)→(1,3)→(2,4)→(3,3)→…,那么质点第20次移动到达的位置的坐标是( )| A. | (9,11) | B. | (11,11) | C. | (10,10) | D. | (10,12) |
7.已知一个等腰三角形的两边长是3cm和7cm,则它的周长为( )
| A. | 13cm | B. | 17cm | C. | 13或17cm | D. | 10cm |
8.方程20x+15y=316的正整数解的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 无数 |
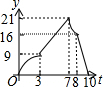
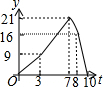
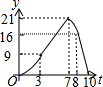
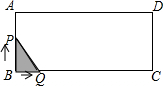 矩形ABCD中,AB=6,BC=8,动点P从点B出发以每秒2个单位长的速度沿BA-AD-DCD的方向运动到C点停止,动点Q以每秒1个单位的速度沿BC方向运动到C点停止,假设P、两点同时出发,运动时间是t秒,y=S△PBQ,则y与t的函数图象大致是( )
矩形ABCD中,AB=6,BC=8,动点P从点B出发以每秒2个单位长的速度沿BA-AD-DCD的方向运动到C点停止,动点Q以每秒1个单位的速度沿BC方向运动到C点停止,假设P、两点同时出发,运动时间是t秒,y=S△PBQ,则y与t的函数图象大致是( )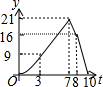
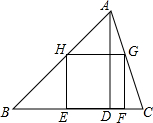 如图,AD是△ABC的高,点E、F在BC边上,点G在AC边上,点H在BC边上,BC=21cm,高AD=15cm,四边形EFGH是△ABC内接正方形,
如图,AD是△ABC的高,点E、F在BC边上,点G在AC边上,点H在BC边上,BC=21cm,高AD=15cm,四边形EFGH是△ABC内接正方形,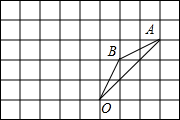 如图所示,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图所示,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.