题目内容
15.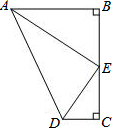 如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°;②∠ADE=∠AEB;③S梯形ABCD=AD•CE;④AD=2AE,四个结论中成立的是( )
如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°;②∠ADE=∠AEB;③S梯形ABCD=AD•CE;④AD=2AE,四个结论中成立的是( )| A. | ①②④ | B. | ①②③ | C. | ②③④ | D. | ①③④ |
分析 过E作EF⊥AD于F,由AAS证明△AEF≌△AEB,得出BE=EF,AB=AF,∠AEF=∠AEB;证出EC=EF=BE,由HL证明Rt△EFD≌Rt△ECD,得出DC=DF,∠FED=∠CED,由平角定义得出∠AED=90°,①正确;
由直角三角形的两个锐角互余得出∠ADE=∠AEB,②正确;
证出AD=AF+FD=AB+DC,得出S梯形ABCD=$\frac{1}{2}$(AB+CD)BC=AD•CE,③正确;
只有∠ADE=30°时,AD=2AE,④不正确;即可得出结论.
解答 解:过E作EF⊥AD于F,如图,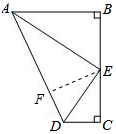
∵AB⊥BC,DC⊥BC,AE平分∠BAD,
∴∠C=∠AFE=∠DFE=∠B=90°,∠FAE=∠BAE,
在△AEF和△AEB中,$\left\{\begin{array}{l}{∠AFE=∠B}&{\;}\\{∠FAE=∠BAE}&{\;}\\{AE=AE}&{\;}\end{array}\right.$,
∴△AEF≌△AEB(AAS),
∴BE=EF,AB=AF,∠AEF=∠AEB;
∵点E是BC的中点,
∴EC=EF=BE,
在Rt△EFD和Rt△ECD中,$\left\{\begin{array}{l}{DE=DE}\\{EF=EC}\end{array}\right.$,
∴Rt△EFD≌Rt△ECD(HL),
∴DC=DF,∠FED=∠CED,
∵∠AEB+∠AEF+∠FED+∠CED=180°,
∴∠AED=$\frac{1}{2}$×180°=90°,①正确;
∵EF⊥AD,
∴∠AEF=∠ADE,
∴∠ADE=∠AEB,②正确;
∵AD=AF+FD=AB+DC,S梯形ABCD=$\frac{1}{2}$(AB+CD)BC=AD•CE,③正确;
只有∠ADE=30°时,AD=2AE,
∴④不正确;
故选:B.
点评 本题考查了梯形的性质、三角形全等的判定与性质、直角三角形的性质;证明三角形全等是解决问题的关键.

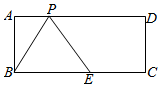 如图,在长方形ABCD中,AB=4,BC=9,点E在BC上,且BE=5,P是长方形ABCD边上的一个动点,在点P运动的过程中,使△PBE为等腰三角形的点P位置共有( )
如图,在长方形ABCD中,AB=4,BC=9,点E在BC上,且BE=5,P是长方形ABCD边上的一个动点,在点P运动的过程中,使△PBE为等腰三角形的点P位置共有( )| A. | 6处 | B. | 5处 | C. | 4处 | D. | 3处 |
| A. | (0,6) | B. | (2,0) | C. | (-2,0) | D. | (0,-2) |
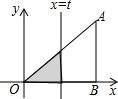 如图所示,在直角△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得的阴影部分面积是S,则S与t之间的函数关系式是S=$\frac{1}{2}$t2(0≤t≤3).
如图所示,在直角△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得的阴影部分面积是S,则S与t之间的函数关系式是S=$\frac{1}{2}$t2(0≤t≤3).
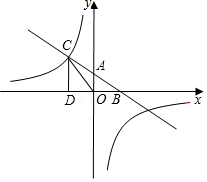 如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}$x+n与x轴,y轴分别交于B,A两点,与反比例函数y=$\frac{k}{x}$交于点C,过点C作CD⊥x轴于点D,已知OB=4,OD=2.
如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}$x+n与x轴,y轴分别交于B,A两点,与反比例函数y=$\frac{k}{x}$交于点C,过点C作CD⊥x轴于点D,已知OB=4,OD=2.