题目内容
12.已知a,b,c满足|a-$\sqrt{18}$|+$\sqrt{b-7}$+(c-$\sqrt{32}$)2=0(1)求a,b,c的值.
(2)试问以a,b,c为边能否构成三角形?如果能构成三角形,请求出三角形的周长;如果不能,请说明理由.
分析 (1)直接利用绝对值以及二次根式和偶次方的性质化简得出答案;
(2)利用三角形三边关系得出能构成三角形,进而得出三角形的周长.
解答 解:(1)∵|a-$\sqrt{18}$|+$\sqrt{b-7}$+(c-$\sqrt{32}$)2=0,
∴a-$\sqrt{18}$=0,$\sqrt{b-7}$=0,c-$\sqrt{32}$=0,
解得:a=3$\sqrt{2}$,b=7,c=4$\sqrt{2}$;
(2)∵a+c=7$\sqrt{2}$,
∴a+c>b,
∴以a,b,c为边能构成三角形,
此时三角形的周长为:7$\sqrt{2}$+7.
点评 此题主要考查了三角形的三边关系以及绝对值以及二次根式和偶次方的性质等知识,正确掌握相关性质是解题关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 如图,点E为BC的中点,若∠B=∠AEF=∠C=90°.连接AF
如图,点E为BC的中点,若∠B=∠AEF=∠C=90°.连接AF

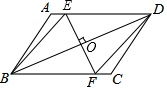 如图,在平行四边形ABCD中,点O是对角线BD的中点,过O点作EF⊥BD,交AD于E,交BC于F,那么,四边形EBFD是菱形吗?为什么?
如图,在平行四边形ABCD中,点O是对角线BD的中点,过O点作EF⊥BD,交AD于E,交BC于F,那么,四边形EBFD是菱形吗?为什么?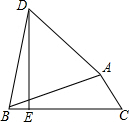 如图,△ABC中,∠C=60°,以AB为边作等边△ABD,过D作DE⊥BC于E.若AC=4,BC=13,则EC=10.5.
如图,△ABC中,∠C=60°,以AB为边作等边△ABD,过D作DE⊥BC于E.若AC=4,BC=13,则EC=10.5.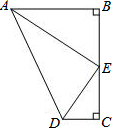 如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°;②∠ADE=∠AEB;③S梯形ABCD=AD•CE;④AD=2AE,四个结论中成立的是( )
如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°;②∠ADE=∠AEB;③S梯形ABCD=AD•CE;④AD=2AE,四个结论中成立的是( )