题目内容
7．
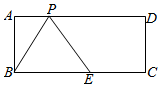如图，在长方形ABCD中，AB=4，BC=9，点E在BC上，且BE=5，P是长方形ABCD边上的一个动点，在点P运动的过程中，使△PBE为等腰三角形的点P位置共有（ ）| A． | 6处 | B． | 5处 | C． | 4处 | D． | 3处 |
分析 作BE的垂直平分线与AD交于点P1，则P1B=P1E；由于AB=5，以点B为圆心，5为半径画弧与AD只有一个交点P2，则BP2=BE；由于AB=4，则以E为圆心，5为半径画弧于AD有两个交点P3和P4，由于CE=4，所以与CD有一个交点P5．
解答 解：作BE的垂直平分线与AD交于点P1；以点B为圆心，5为半径画弧交AD于点P2；以E为圆心，5为半径画弧交AD于P3、P4，交CD于P5，如图，
所以△PBE为等腰三角形的点P位置共有5处．
故选B．
点评 本题考查了矩形的性质：平行四边形的性质矩形都具有；矩形的四个角都是直角．也考查了等腰三角形的判定与分类讨论数学的应用．
练习册系列答案
科学实验活动册系列答案
相关题目
用4个小立方块搭成如图所示的几何体，该几何体从正面看到的图形是（ ）
15．
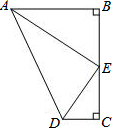如图，点E是BC的中点，AB⊥BC，DC⊥BC，AE平分∠BAD，下列结论：①∠AED=90°；②∠ADE=∠AEB；③S梯形ABCD=AD•CE；④AD=2AE，四个结论中成立的是（ ）
如图，点E是BC的中点，AB⊥BC，DC⊥BC，AE平分∠BAD，下列结论：①∠AED=90°；②∠ADE=∠AEB；③S梯形ABCD=AD•CE；④AD=2AE，四个结论中成立的是（ ）| A． | ①②④ | B． | ①②③ | C． | ②③④ | D． | ①③④ |
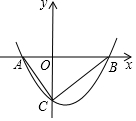平面直角坐标系中，将抛物线y=ax2经平移后与x轴交于点A、B，与y轴交于点C，若$\frac{{{S_{△AOC}}}}{{{S_{△BOC}}}}=\frac{{\sqrt{5}-1}}{2}$，则称平移后的抛物线所在的位置为抛物线y=ax2在该平面直角坐标系中的一个“黄金位”．如图所示的抛物线为抛物线y=ax2的一个“黄金位”，且AB=2，将图中的抛物线向右平移$\frac{5+\sqrt{5}}{2}$个单位长度又可得到抛物线y=ax2的另一个“黄金位”．
16．如图给出了四组三角形，其中全等的三角形有（ ）组．
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |