题目内容
若
=
=
=k,则k= .
| a+b |
| c |
| b+c |
| a |
| c+a |
| b |
考点:比例的性质
专题:
分析:根据比例的性质得到a+b=ck ①,b+c=ak ②,c+a=bk ③,利用这三个等式相加来求k的值.
解答:解:根据已知条件,得出
a+b=ck ①,
b+c=ak ②,
c+a=bk ③,
①+②+③,得 2(a+b+c)=k(a+b+c).
(1)当a+b+c≠0,则k=2;
(2)当a+b+c=0,则a+b=-c,b+c=-a,a+c=-b,
∴k=-1;
综上所述,k的值是2或-1.
故答案是:2或-1.
a+b=ck ①,
b+c=ak ②,
c+a=bk ③,
①+②+③,得 2(a+b+c)=k(a+b+c).
(1)当a+b+c≠0,则k=2;
(2)当a+b+c=0,则a+b=-c,b+c=-a,a+c=-b,
∴k=-1;
综上所述,k的值是2或-1.
故答案是:2或-1.
点评:本题考查了比例的性质.组成比例的四个数,叫做比例的项.两端的两项叫做比例的外项,中间的两项叫做比例的内项.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
下列图形中,不是正方体表面展开图的图形的个数是( )


| A、1个 | B、2个 | C、3个 | D、4个 |
数-5与-4的和比它们的绝对值的和( )
| A、大9 | B、小9 | C、小18 | D、相等 |

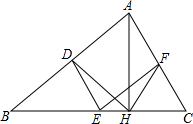 如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.