已知a-b=3.a-c=$\root{3}{26}$.求2+2]的值．题目和参考答案——青夏教育精英家教网—

题目内容

14．已知a-b=3，a-c=$\root{3}{26}$，求（c-b）[（a-b）²+（a-c）（a-b）+（a-c）²]的值．

分析两式相减求出c-b的值，代入后根据立方和公式求出即可．

解答解：∵a-b=3，a-c=$\root{3}{26}$，
∴c-b=3-$\root{3}{26}$，
∴（c-b）[（a-b）²+（a-c）（a-b）+（a-c）²]
=（3-$\root{3}{26}$）[3²+$\root{3}{26}$×3+（$\root{3}{26}$）²]
=3³-（$\root{3}{26}$）³
=27-25
=1．

点评本题考查了立方和公式和整式的混合运算的应用，能正确运用公式进行计算是解此题的关键，注意：（a-b）（a²+ab+b²）=a³-b³．

练习册系列答案

5．繁昌四中为了了解学生对三种国庆活动方案的意见，对全体学生进行了一次抽样调查（被调查学生至多赞成其中的一种方案），现将调查结果绘制成如图两幅不完整的统计图，请根据图中提供的信息解答下列问题

（1）这次共调查了多少名学生？扇形统计图中方案1所对应的圆心角的度数为多少度？
（2）请把条形统计图补充完整；
（3）已知繁昌四中约有1500名学生，试估计该校赞成方案1的学生约有多少人？

2．

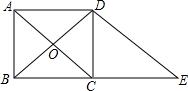如图，在矩形ABCD中，对角线AC、BD相交于点O，过点D作DE∥AC，交BC的延长线于点E．求证：BD=DE．

9．

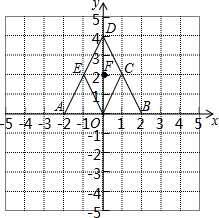如图，指出坐标平面内各点的坐标：A（-2，0），C（1，2），F（0，2）．

19．解方程：
（1）5（x+2）=2（5x-1）；
（2）（x+1）-2（x-1）=1-3x；
（3）3-2（x+1）=2（x-3）；
（4）4（2x-1）-3（5x+1）=14；
（5）2（2x+1）=3（x+2）-（x+6）；
（6）3（x+1）-$\frac{1}{3}$（x-1）=4（x-1）-$\frac{7}{2}$（x+1）．

6．解方程：x²-2x-2$\sqrt{2}$x+3+2$\sqrt{2}$=0．

3．抛物线y=ax²与直线y=2x+1交于点（1，m），求抛物线的解析式．

4．若关于x的方程x²+（k-2）x+k²=0的两根互为倒数，则k为（　　）

试题分类