题目内容
11.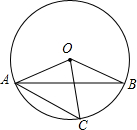 如图,在⊙O中,AB是弦,C是$\widehat{AB}$上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的大小为30度.
如图,在⊙O中,AB是弦,C是$\widehat{AB}$上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的大小为30度.
分析 由∠BAO=25°,利用等腰三角形的性质,可求得∠AOB的度数,又由∠OCA=40°,可求得∠CAO的度数,继而求得∠AOC的度数,则可求得答案.
解答 解:∵∠BAO=25°,OA=OB,
∴∠B=∠BAO=25°,
∴∠AOB=180°-∠BAO-∠B=130°,
∵∠ACO=40°,OA=OC,
∴∠C=∠CAO=40°,
∴∠AOC=180°-∠CAO-∠C=100°,
∴∠BOC=∠AOB-∠AOC=30°.
故答案为30°.
点评 本题考查了圆周角定理以及等腰三角形的性质.注意利用等腰三角形的性质求解是关键.

练习册系列答案
相关题目
1.已知点(-4,y1),(2,y2)都在直线y=-2x+3上,则y1,y2大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
16.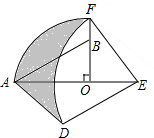 如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )
如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )
 如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )
如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )| A. | π | B. | $\frac{5π}{4}$ | C. | 3+π | D. | 8-π |
12.已知一个平行四边形两邻边的长分别为6和10,那么它的周长为( )
| A. | 16 | B. | 30 | C. | 32 | D. | 60 |
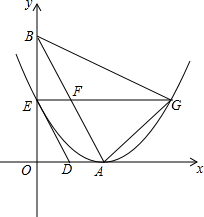 如图,直线y=-$\sqrt{3}$x+2$\sqrt{3}$与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和$\sqrt{3}$个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
如图,直线y=-$\sqrt{3}$x+2$\sqrt{3}$与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和$\sqrt{3}$个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.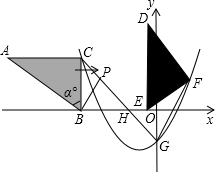 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-8,3),B(-4,0),C(-4,3),∠ABC=α°.抛物线y=$\frac{1}{2}$x2+bx+c经过点C,且对称轴为x=-$\frac{4}{5}$,并与y轴交于点G.
如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-8,3),B(-4,0),C(-4,3),∠ABC=α°.抛物线y=$\frac{1}{2}$x2+bx+c经过点C,且对称轴为x=-$\frac{4}{5}$,并与y轴交于点G.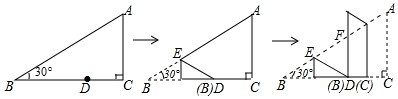
 如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是24.
如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是24. 如图,四边形OABC的边OA,OC分别在y轴、x轴的正半轴,已知:A(0,4),B(4,3),C(4,0).
如图,四边形OABC的边OA,OC分别在y轴、x轴的正半轴,已知:A(0,4),B(4,3),C(4,0).