题目内容
16.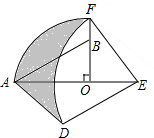 如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )
如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )| A. | π | B. | $\frac{5π}{4}$ | C. | 3+π | D. | 8-π |
分析 作DH⊥AE于H,根据勾股定理求出AB,根据阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积-扇形DEF的面积、利用扇形面积公式计算即可.
解答 解: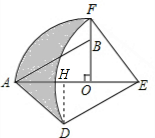 作DH⊥AE于H,
作DH⊥AE于H,
∵∠AOB=90°,OA=3,OB=2,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{13}$,
由旋转的性质可知,OE=OB=2,DE=EF=AB=$\sqrt{13}$,△DHE≌△BOA,
∴DH=OB=2,
阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积-扇形DEF的面积
=$\frac{1}{2}$×5×2+$\frac{1}{2}$×2×3+$\frac{90×π×{3}^{2}}{360}$-$\frac{90×π×13}{360}$
=8-π,
故选:D.
点评 本题考查的是扇形面积的计算、旋转的性质、全等三角形的性质,掌握扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$和旋转的性质是解题的关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
7.已知点(a-1,y1)、(a+1,y2)在反比例函数y=$\frac{k}{x}$(k>0)的图象上,若y1<y2,则a的范围是( )
| A. | a>1 | B. | a<-1 | C. | -1<a<1 | D. | -1<a<0或0<a<1 |
 自主学习,请阅读下列解题过程.
自主学习,请阅读下列解题过程.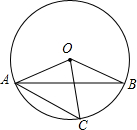 如图,在⊙O中,AB是弦,C是$\widehat{AB}$上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的大小为30度.
如图,在⊙O中,AB是弦,C是$\widehat{AB}$上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的大小为30度. 如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB
如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB