题目内容
19．同时抛掷A、B两个均匀的小立方体（每个面上分别标有数字1，2，3，4，5，6），设两立方体朝上的数字分别为x、y，并以此确定点P（x，y），请用树状图或列表法求出点P落在抛物线y=-x2+3x上的概率．分析 首先根据题意列出表格，然后由表格即可求得所有等可能的结果与点P落在抛物线y=-x2+3x上的情况，再利用概率公式即可求得答案．
解答 解：列表得：
| （1，6） | （2，6） | （3，6） | （4，6） | （5，6） | （6，6） |
| （1，5） | （2，5） | （3，5） | （4，5） | （5，5） | （6，5） |
| （1，4） | （2，4） | （3，4） | （4，4） | （5，4） | （6，4） |
| （1，3） | （2，3） | （3，3） | （4，3） | （5，3） | （6，3） |
| （1，2） | （2，2） | （3，2） | （4，2） | （5，2） | （6，2） |
| （1，1） | （2，1） | （3，1） | （4，1） | （5，1） | （6，1） |
∴点P落在抛物线y=-x2+3x上的概率为$\frac{1}{18}$．
点评 此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
10．已知，两个图形成轴对称，则这两个图形（ ）
| A． | 全等 | B． | 不一定全等 | C． | 面积不一样大 | D． | 周长不一样 |
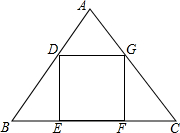如图，在△ABC中，AB=AC，正方形DEFG的顶点D、G分别在AB、AC上，EF在BC上，设AB=5，BC=6，求正方形DEFG的边长．
如图，在旧城改造中，要拆除一建筑物AB，在地面上事先划定以B为圆心，半径与AB等长的圆形危险区．现在从离点B 24m远的建筑物CD的顶端C测得点A的仰角为45°，点B的俯角为30°，问离点B 35m处的一保护文物是否在危险区内？
如图所示，在矩形ABCD的顶点A处拴了一只小羊，在B、C、D处各有一筐青草，要使小羊至少能吃到一筐子里的草．如果AB=5，BC=12，则拴羊绳的长l最少是5．