题目内容
9.若△ABC的三边a、b、c满足a2-6a+b2-10b+c2-8c+50=0,求△ABC的周长?分析 利用一次项的系数分别求出常数项,把50分成9、16、25,然后与(a2-6a)、(b2-8b)、(c2-10c)分别组成完全平方公式,再利用非负数的性质,可分别求出a、b、c的值,进一步求得△ABC的周长.
解答 解:∵a2-6a+b2-10b+c2-8c+50=0,
∴a2-6a+9+b2-8b+16+c2-10c+25=0,
即(a-3)2+(b-4)2+(c-5)2=0,
∴a=3,b=4,c=5,
∴△ABC的周长=3+4+5=12.
点评 本题考查了配方法的应用、勾股定理、非负数的性质,解题的关键是注意配方法的步骤,在变形的过程中不要改变式子的值.

练习册系列答案
相关题目
4.已知2x2+3x+1的值是10,则代数式4x2+6x+1的值是( )
| A. | 10 | B. | 0 | C. | 19 | D. | 20 |
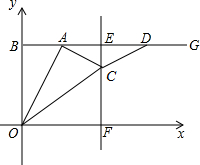 如图,在平面直角坐标系中,以点B(0,8)为端点的射线BG∥x轴,点A是射线BG上的一个动点(点A与点B不重合).在射线AG上取AD=OB,作线段AD的垂直平分线,垂足为E,且与x轴交于点F,过点A作AC⊥OA,交射线EF于点C.连接OC、CD,设点A的横坐标为t.
如图,在平面直角坐标系中,以点B(0,8)为端点的射线BG∥x轴,点A是射线BG上的一个动点(点A与点B不重合).在射线AG上取AD=OB,作线段AD的垂直平分线,垂足为E,且与x轴交于点F,过点A作AC⊥OA,交射线EF于点C.连接OC、CD,设点A的横坐标为t. 如图,化简|a+b|-|a|+|b|=2a+2b.
如图,化简|a+b|-|a|+|b|=2a+2b.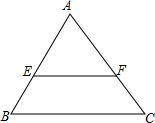 如图,△ABC中,EF∥BC,且EF=$\frac{2}{3}$BC=4cm,△AEF的周长为10cm,求BCFE的周长.
如图,△ABC中,EF∥BC,且EF=$\frac{2}{3}$BC=4cm,△AEF的周长为10cm,求BCFE的周长.