题目内容
9．
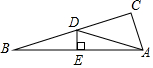如图，在△ABC中，∠C=90°，点E是斜边AB的中点，ED⊥AB，且∠CAD：∠BAD=5：2，则∠BAC=70°．
分析 先根据题意得出ED是AB的垂直平分线，故可得出∠BAD=∠B．根据∠CAD：∠BAD=5：2可设∠CAD=5x，则∠BAD=∠B=2x，再由三角形内角和定理求出x的值，进而可得出结论．
解答 解：∵点E是AB的中点且ED⊥AB，
∴ED是AB的垂直平分线，
∴∠BAD=∠B．
∵∠CAD：∠BAD=5：2，
∴设∠CAD=5x，则∠BAD=∠B=2x，
∴5x+2x+2x=90°，
∴x=10°，
∴∠BAC=∠CAD+∠BAD=5x+2x=7x=70°．
故答案为：70°．
点评 本题考查的是线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．
练习册系列答案
相关题目
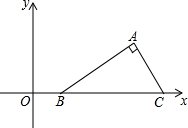在平面直角坐标系中，Rt△ABC的斜边BC在x轴上，点B的坐标为（1，0），AC=2，∠ABC=30°，把Rt△ABC先绕点B顺时针旋转180°，然后向下平移2个单位，则点A的对应点D的坐标为（-2，-2-$\sqrt{3}$）．
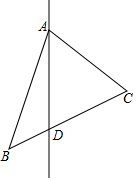如图．已知△ABC．点D在BC边上．过点A作直线AD．
14．
一个有进水管和出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分钟的进水量和出水量是两个常数，容器内的水量y（L）与时间x（min）之间的关系如图所示，则每分钟的出水量为（ ）
一个有进水管和出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分钟的进水量和出水量是两个常数，容器内的水量y（L）与时间x（min）之间的关系如图所示，则每分钟的出水量为（ ）| A． | 5L | B． | 3.75L | C． | 2.5L | D． | 1.25L |
1．下列计算正确的是（ ）
| A． | a3•a2=a6 | B． | （-2a2）3=-8a6 | C． | （a+b）2=a2+b2 | D． | 2a+3a=5a2 |