题目内容
4.△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,且c2-4ac+4a2=0,则sinA+cosA的值为( )| A. | $\frac{1+\sqrt{3}}{2}$ | B. | $\frac{1+\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}+\sqrt{3}}{2}$ | D. | $\sqrt{2}$ |
分析 根据c2-4ac+4a2=0,可以求得a与c的关系,由△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,可以得到a与b的关系,从而可以解答本题.
解答 解:∵c2-4ac+4a2=0,
∴(c-2a)2=0
∴c=2a,
∵在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,
∴b=$\sqrt{3}a$,
∴sinA+cosA=$\frac{a}{c}+\frac{b}{c}$=$\frac{1}{2}+\frac{\sqrt{3}}{2}=\frac{1+\sqrt{3}}{2}$,
故选A.
点评 本题考查因式分解的应用、解直角三角形,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.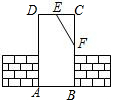 如图工人师傅砌门常用木条EF固定长方形门框ABCD,使其不变形的根据( )
如图工人师傅砌门常用木条EF固定长方形门框ABCD,使其不变形的根据( )
 如图工人师傅砌门常用木条EF固定长方形门框ABCD,使其不变形的根据( )
如图工人师傅砌门常用木条EF固定长方形门框ABCD,使其不变形的根据( )| A. | 两点之间线段最短 | B. | 长方形的对称性 | ||
| C. | 长方形的四个角都是直角 | D. | 三角形的稳定性 |
15.下列给出的四组数中,是勾股数的一组是( )
| A. | 1、2、3 | B. | 1、2、$\sqrt{3}$ | C. | 5、12、10 | D. | 6、8、10 |
16.下列各数中为正数的是( )
| A. | -|-3| | B. | -32 | C. | (-3)2 | D. | (-3)3 |
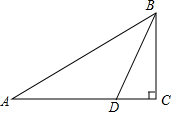 如图,为了测出某塔BC的高度,在塔前的平地上选择一点A,用测角仪测得塔顶B的仰角为30°,在A、C之间选择一点D(A、D、C三点在同一直线上),用测角仪测得塔顶B的仰角为75°,且A、D间的距离为36m.求塔高BC(结果用根号表示).
如图,为了测出某塔BC的高度,在塔前的平地上选择一点A,用测角仪测得塔顶B的仰角为30°,在A、C之间选择一点D(A、D、C三点在同一直线上),用测角仪测得塔顶B的仰角为75°,且A、D间的距离为36m.求塔高BC(结果用根号表示). 如图所示,已知点A的坐标为(1,0),C,B两点分别在x轴、y轴上移动,且∠1=45°,则点B坐标为(0,-$\sqrt{2}$)时,BC与⊙O相切.
如图所示,已知点A的坐标为(1,0),C,B两点分别在x轴、y轴上移动,且∠1=45°,则点B坐标为(0,-$\sqrt{2}$)时,BC与⊙O相切.