题目内容
6.下列关于x的一元二次方程中,有两个不相等的实数根的是( )| A. | x2+3=0 | B. | x2-4x+4=0 | C. | x2-2014=0 | D. | x2+2x+3=0 |
分析 直接利用根的判别式△=b2-4ac,进行判定,即可求得答案.
解答 解:A、∵x2+3=0,
∴x2=-3,故无实数根;
B、∵x2-4x+4=0,
∴△=(-4)2-4×1×4=0,故有两个不相等的实数根;
C、∵x2-2014=0,
∴△=0-4×1×(-2014)=8056>0,故有两个不相等的实数根;
D、∵x2+2x+3=0,
∴△=22-4×1×3=-8<0,故无实数根.
故选C.
点评 此题考查了根的判别式.注意△>0?方程有两个不相等的实数根.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
17.下列说法错误的是( )
| A. | 单项式x的系数和次数都是1 | |
| B. | $\frac{1}{2}$不是单项式 | |
| C. | 多项式3x2y+2xy-3x+y中一次项的系数分别是-3,1 | |
| D. | -$\frac{2xy}{3}$是系数为-$\frac{2}{3}$的二次单项式 |
11. 如图,∠AOC=∠BOD=90°,∠AOD=140°,则∠BOC的度数为( )
如图,∠AOC=∠BOD=90°,∠AOD=140°,则∠BOC的度数为( )
 如图,∠AOC=∠BOD=90°,∠AOD=140°,则∠BOC的度数为( )
如图,∠AOC=∠BOD=90°,∠AOD=140°,则∠BOC的度数为( )| A. | 30° | B. | 45° | C. | 50° | D. | 40° |
18.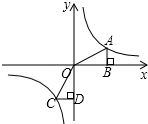 如图,A,C是函数$y=\frac{1}{x}$的图象上任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记Rt△OAB的面积为S1,Rt△COD的面积S2,则( )
如图,A,C是函数$y=\frac{1}{x}$的图象上任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记Rt△OAB的面积为S1,Rt△COD的面积S2,则( )
 如图,A,C是函数$y=\frac{1}{x}$的图象上任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记Rt△OAB的面积为S1,Rt△COD的面积S2,则( )
如图,A,C是函数$y=\frac{1}{x}$的图象上任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记Rt△OAB的面积为S1,Rt△COD的面积S2,则( )| A. | S1>S2 | B. | S1=S2 | C. | S1<S2 | D. | S1≥S2 |
 如图,已知点P在AB上,∠APD=∠APC,∠DBA=∠CBA,求证:AC=AD.
如图,已知点P在AB上,∠APD=∠APC,∠DBA=∠CBA,求证:AC=AD.
 如图,在△ABC中,D为三角形内一点,∠A=35°,∠ABD=20°,∠ACD=25°,BD∥CE,则∠DCE=75°.
如图,在△ABC中,D为三角形内一点,∠A=35°,∠ABD=20°,∠ACD=25°,BD∥CE,则∠DCE=75°. 如图,在△ABC中,∠1=∠2,∠3=∠4,∠A=65°,则∠F=122.5°.
如图,在△ABC中,∠1=∠2,∠3=∠4,∠A=65°,则∠F=122.5°.