题目内容
 如图,直线y=-x+3与x轴交于点A,与y轴交于点B,抛物线y=-x2+bx+c经过点A、B.
如图,直线y=-x+3与x轴交于点A,与y轴交于点B,抛物线y=-x2+bx+c经过点A、B.(1)求抛物线的解析式;
(2)在第一象限的抛物线上,是否存在一点P,使得△ABP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.
(3)点M在抛物线上,过点M作y轴的平行线交直线AB于点N,是否存在以点M、N、O、B为顶点的平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)根据直线的解析式求得直线与坐标轴的交点坐标,然后代入抛物线的解析式利用待定系数法确定解析式即可;
(2)假设存在点P(x,y)使得△ABP的面积最大,连接OP,利用S△ABP=S△OPA+S△OPB-S△OAB得到有关面积与点P的横坐标的关系即可确定M点的坐标;
(3)存在,设点M(x,y),所以yM=-x2+2x+3,根据MN∥y轴得到yN=-x+3,从而表示出MN=|(-x+3)-(-x2+2x+3)|=|x2-3x|,利用等腰三角形的性质得到当MN=BO=3时,以M、N、O、B为顶点的四边形是平行四边形,从而得到|x2-3x|=3,求得x的值即可求得点M的坐标.
(2)假设存在点P(x,y)使得△ABP的面积最大,连接OP,利用S△ABP=S△OPA+S△OPB-S△OAB得到有关面积与点P的横坐标的关系即可确定M点的坐标;
(3)存在,设点M(x,y),所以yM=-x2+2x+3,根据MN∥y轴得到yN=-x+3,从而表示出MN=|(-x+3)-(-x2+2x+3)|=|x2-3x|,利用等腰三角形的性质得到当MN=BO=3时,以M、N、O、B为顶点的四边形是平行四边形,从而得到|x2-3x|=3,求得x的值即可求得点M的坐标.
解答: 解:(1)直线y=-x+3,当y=0时,x=3;当x=0时,y=3,
解:(1)直线y=-x+3,当y=0时,x=3;当x=0时,y=3,
∴A(3,0)、B(0,3),
∵抛物线过A(3,0)、B(0,3),
∴
解得:
,
∴所求抛物线的解析式为y=-x2+2x+3;
(2)假设存在点P(x,y)使得△ABP的面积最大,
连接OP,则S△ABP=S△OPA+S△OPB-S△OAB=
OA•y+
OB•x-
OA•OB
=
y+
x-
=
(x-x2+2x+3)-
=-
(x2-3x)
=-
(x-
)2+
当x=
时,点P(
,
)在第一象限,此时△ABP的面积最大,
所求的点P的坐标为:P(
,
).
(3)存在,设点M(x,y),所以yM=-x2+2x+3
∵MN∥y轴,
∴yN=-x+3,
∴MN=|(-x+3)-(-x2+2x+3)|=|x2-3x|
当MN=BO=3时,
以M、N、O、B为顶点的四边形是平行四边形,
即|x2-3x|=3,
解得:x=
或x=
当x=
时,y=-
,
当x=
时,y=-
,
所以当M(
,-
)或M(
,-
)以M、N、O、B为顶点的四边形是平行四边形.
 解:(1)直线y=-x+3,当y=0时,x=3;当x=0时,y=3,
解:(1)直线y=-x+3,当y=0时,x=3;当x=0时,y=3,∴A(3,0)、B(0,3),
∵抛物线过A(3,0)、B(0,3),
∴
|
解得:
|
∴所求抛物线的解析式为y=-x2+2x+3;
(2)假设存在点P(x,y)使得△ABP的面积最大,
连接OP,则S△ABP=S△OPA+S△OPB-S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
当x=
| 3 |
| 2 |
| 3 |
| 2 |
| 15 |
| 4 |
所求的点P的坐标为:P(
| 3 |
| 2 |
| 15 |
| 4 |
(3)存在,设点M(x,y),所以yM=-x2+2x+3
∵MN∥y轴,
∴yN=-x+3,
∴MN=|(-x+3)-(-x2+2x+3)|=|x2-3x|
当MN=BO=3时,
以M、N、O、B为顶点的四边形是平行四边形,
即|x2-3x|=3,
解得:x=
3+
| ||
| 2 |
3-
| ||
| 2 |
当x=
3+
| ||
| 2 |
3+
| ||
| 2 |
当x=
3-
| ||
| 2 |
3-
| ||
| 2 |
所以当M(
3+
| ||
| 2 |
3+
| ||
| 2 |
3-
| ||
| 2 |
3-
| ||
| 2 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知非负数a,b,c满足a+b=2,c-3a=4,设S=a2+b+c的最大值为m,最小值为n,则m-n的值为( )
| A、9 | ||
| B、8 | ||
| C、1 | ||
D、
|
 如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )
如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )| A、25πcm2 |
| B、49πcm2 |
| C、32πcm2 |
| D、36πcm2 |
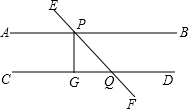 如图,AB∥CD,直线EF分别与直线AB和直线CD相交于点P和点Q,PG⊥CD于G,若∠APE=48°,则∠QPG的度数为( )
如图,AB∥CD,直线EF分别与直线AB和直线CD相交于点P和点Q,PG⊥CD于G,若∠APE=48°,则∠QPG的度数为( )| A、42° | B、46° |
| C、32° | D、36° |
 如图,在矩形纸片ABCD中,AB=6,BC=8,把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G,E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE 沿EF折叠,使点D落在D′处,点D′恰好与点A重合.
如图,在矩形纸片ABCD中,AB=6,BC=8,把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G,E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE 沿EF折叠,使点D落在D′处,点D′恰好与点A重合. 李明乘车从永康到某景区旅游,同时王红从该景区返回永康.线段OB表示李明离永康的路程S1(km)与时间t(h)的函数关系;线段AC表示王红离永康的路程S2(km)与时间t(h)的函数关系.行驶1小时,李明、王红离永康的路程分别为100km、280km,王红从景区返回永康用了4.5小时.(假设两人所乘的车在同一线路上行驶)
李明乘车从永康到某景区旅游,同时王红从该景区返回永康.线段OB表示李明离永康的路程S1(km)与时间t(h)的函数关系;线段AC表示王红离永康的路程S2(km)与时间t(h)的函数关系.行驶1小时,李明、王红离永康的路程分别为100km、280km,王红从景区返回永康用了4.5小时.(假设两人所乘的车在同一线路上行驶) 如图所示,点D为△ABC的边AB的中点,且AD=CD.求证:∠ACB=90°.
如图所示,点D为△ABC的边AB的中点,且AD=CD.求证:∠ACB=90°.