题目内容
5.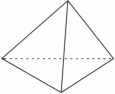 如图,有一个质地均匀的正四面体,其四个面上分别画着圆、等边三角形、菱形、正五边形,投掷该正四面体一次,向下的一面的图形既是轴对称图形又是中心对称图形的概率是( )
如图,有一个质地均匀的正四面体,其四个面上分别画着圆、等边三角形、菱形、正五边形,投掷该正四面体一次,向下的一面的图形既是轴对称图形又是中心对称图形的概率是( )| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
分析 先根据轴对称图形和中心对称图形的定义得到圆和菱形既是轴对称图形又是中心对称图形,然后根据概率公式求解.
解答 解:投掷该正四面体一次,向下的一面的图形既是轴对称图形又是中心对称图形的概率=$\frac{2}{4}$=$\frac{1}{2}$.
故选D.
点评 本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.也考查了轴对称图形和中心对称图形.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
15.不等式(a-2012)x>a-2012的解集是x<1.则a应满足的条件是( )
| A. | a=2012 | B. | a<2012 | C. | a>2012 | D. | 无法确定 |
16.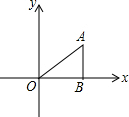 如图,在△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1.将△ABO绕O点旋转90°后得到△A1B1O,则点A1的坐标为( )
如图,在△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1.将△ABO绕O点旋转90°后得到△A1B1O,则点A1的坐标为( )
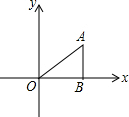 如图,在△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1.将△ABO绕O点旋转90°后得到△A1B1O,则点A1的坐标为( )
如图,在△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1.将△ABO绕O点旋转90°后得到△A1B1O,则点A1的坐标为( )| A. | (-1,$\sqrt{3}$) | B. | (-1,$\sqrt{3}$)或(1,-$\sqrt{3}$) | C. | (-1,-$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$)或(-$\sqrt{3}$,-1) |
14.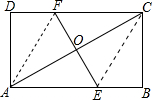 如图,ABCD是矩形纸片,翻折∠B,∠D,使AD,BC边与对角线AC重叠,且顶点B,D恰好落在同一点O上,折痕分别是CE,AF,则$\frac{AE}{EB}$等于( )
如图,ABCD是矩形纸片,翻折∠B,∠D,使AD,BC边与对角线AC重叠,且顶点B,D恰好落在同一点O上,折痕分别是CE,AF,则$\frac{AE}{EB}$等于( )
 如图,ABCD是矩形纸片,翻折∠B,∠D,使AD,BC边与对角线AC重叠,且顶点B,D恰好落在同一点O上,折痕分别是CE,AF,则$\frac{AE}{EB}$等于( )
如图,ABCD是矩形纸片,翻折∠B,∠D,使AD,BC边与对角线AC重叠,且顶点B,D恰好落在同一点O上,折痕分别是CE,AF,则$\frac{AE}{EB}$等于( )| A. | $\sqrt{3}$ | B. | 2 | C. | 1.5 | D. | $\sqrt{2}$ |
4.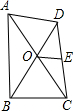 如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O,AO=CO,∠AOD=∠ADO,E是DC边的中点,下列结论中,错误的是( )
如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O,AO=CO,∠AOD=∠ADO,E是DC边的中点,下列结论中,错误的是( )
 如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O,AO=CO,∠AOD=∠ADO,E是DC边的中点,下列结论中,错误的是( )
如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O,AO=CO,∠AOD=∠ADO,E是DC边的中点,下列结论中,错误的是( )| A. | OE=$\frac{1}{2}$AD | B. | OE=$\frac{1}{2}$OB | C. | OE=$\frac{1}{2}$OC | D. | OE=$\frac{1}{2}$BC |
 如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于5π.
如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于5π. 如图,在正三角形ABC中,AD⊥BC于点D,则∠BAD=30°°.
如图,在正三角形ABC中,AD⊥BC于点D,则∠BAD=30°°.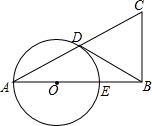 已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.


