题目内容
20. 如图,在正三角形ABC中,AD⊥BC于点D,则∠BAD=30°°.
如图,在正三角形ABC中,AD⊥BC于点D,则∠BAD=30°°.
分析 根据正三角形ABC得到∠BAC=60°,因为AD⊥BC,根据等腰三角形的三线合一得到∠BAD的度数.
解答 解:∵△ABC是等边三角形,
∴∠BAC=60°,
∵AB=AC,AD⊥BC,
∴∠BAD=$\frac{1}{2}$∠BAC=30°,
故答案为:30°.
点评 本题考查的是等边三角形的性质,掌握等边三角形的三个内角都是60°和等腰三角形的三线合一是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.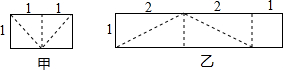 如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
 如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )| A. | 甲、乙都可以 | B. | 甲、乙都不可以 | C. | 甲不可以、乙可以 | D. | 甲可以、乙不可以 |
5.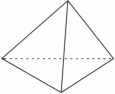 如图,有一个质地均匀的正四面体,其四个面上分别画着圆、等边三角形、菱形、正五边形,投掷该正四面体一次,向下的一面的图形既是轴对称图形又是中心对称图形的概率是( )
如图,有一个质地均匀的正四面体,其四个面上分别画着圆、等边三角形、菱形、正五边形,投掷该正四面体一次,向下的一面的图形既是轴对称图形又是中心对称图形的概率是( )
 如图,有一个质地均匀的正四面体,其四个面上分别画着圆、等边三角形、菱形、正五边形,投掷该正四面体一次,向下的一面的图形既是轴对称图形又是中心对称图形的概率是( )
如图,有一个质地均匀的正四面体,其四个面上分别画着圆、等边三角形、菱形、正五边形,投掷该正四面体一次,向下的一面的图形既是轴对称图形又是中心对称图形的概率是( )| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
12. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )| A. | 50° | B. | 40° | C. | 30° | D. | 25° |
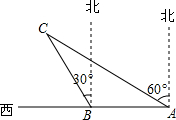 如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:$\sqrt{3}$≈1.732)
如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:$\sqrt{3}$≈1.732) 如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且$\widehat{DA}$=$\widehat{DC}$,连接AC,AD,延长AD交BM于点E.
如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且$\widehat{DA}$=$\widehat{DC}$,连接AC,AD,延长AD交BM于点E.