题目内容
15.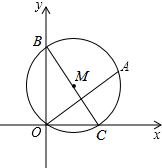 在平面直角坐标系中,点A的坐标是(4,3),动圆M经过A、O,分别与两轴的正半轴交于点B、C,则BC的取值范围是5≤BC<$\frac{25}{3}$.
在平面直角坐标系中,点A的坐标是(4,3),动圆M经过A、O,分别与两轴的正半轴交于点B、C,则BC的取值范围是5≤BC<$\frac{25}{3}$.
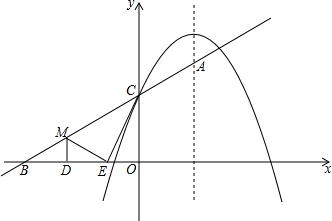
分析 先求出OA=5,由于动圆M经过点A、O.所以OA为直径时,动圆M的直径最小,此时BC=OA=5;当⊙M与x轴切于点O时,动圆M的直径最大,如图2,作AH⊥OE,根据切线的性质得BC为⊙M的直径,则∠BAO=90°,再证明Rt△OAH∽Rt△OBA,利用相似比可计算出OB=$\frac{25}{3}$,即可得出BC的取值范围.
解答 解:作AD⊥x轴于D,如图1所示: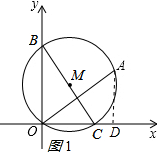 ∵点A的坐标是(4,3),
∵点A的坐标是(4,3),
∴OA=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵∠BOC=90°,
∴BC为动圆M的直径;
当OA为直径时,动圆M的直径最小,此时BC=OA=5;
当⊙M与x轴切于点O时,动圆M的直径BC最大,如图2所示:
作AH⊥OE,
则∠AHO=90°,
∵⊙M与x轴相切,
∴BC为⊙M的直径,
∴∠BAO=90°,
∵∠AOH=∠BOA,
∴Rt△OAH∽Rt△OBA,
∴AO:OB=OH:AO,即5:OB=3:5,
∴OB=$\frac{25}{3}$,
∴BC的取值范围为5≤BC<$\frac{25}{3}$.
点评 本题是圆的综合题,考查了圆周角定理、勾股定理、切线的性质、相似三角形的判定与性质;根据题意得出当OA为直径时,动圆M的直径最小,当⊙M与x轴切于点O时,动圆M的直径BC最大是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在图中直线上找到一点M,使它到A、B两点的距离和最小.
在图中直线上找到一点M,使它到A、B两点的距离和最小. 公路l同侧的A、B两村,共同出资在公路边修建一个客车停靠站C,并使停靠站到A、B两村的距离相等,你如何确定停靠站C的位置.利用尺规作图作出点C,写出作法,并保留作图痕迹.
公路l同侧的A、B两村,共同出资在公路边修建一个客车停靠站C,并使停靠站到A、B两村的距离相等,你如何确定停靠站C的位置.利用尺规作图作出点C,写出作法,并保留作图痕迹.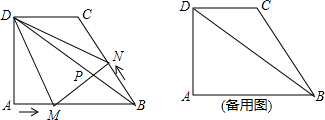
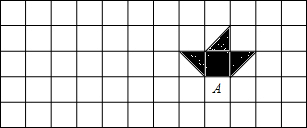 如图所示,图中的小船A是由一艘小船B先向右平移三格,再向上平移2格后得到的,请你画出原来的小船B,并求出此时小船的面积.(图中每一小格的边长为1)
如图所示,图中的小船A是由一艘小船B先向右平移三格,再向上平移2格后得到的,请你画出原来的小船B,并求出此时小船的面积.(图中每一小格的边长为1)