题目内容
9.在△ABC中,AC=3,AB=7,则中线AD的范围是2<AD<5.分析 延长AD到E,使AD=DE,连结BE,证明△ADC≌△EDB就可以得出BE=AC,根据三角形的三边关系就可以得出结论.
解答 解:延长AD到E,使AD=DE,连结BE.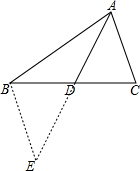
∵AD是△ABC的中线,
∴BD=CD.
在△ADC和△EDB中,
$\left\{\begin{array}{l}{CD=BD}\\{∠ADC=∠EDB}\\{AD=CD}\end{array}\right.$,
∴△ADC≌△EDB(SAS),
∴AC=BE.
∵AB-AE<AE<AB+BE,
∴AB-AC<2AD<AB+AC.
∵AB=7,AC=3,
∴2<AD<5.
故答案为:2<AD<5.
点评 本题考查了全等三角形的判定及性质的运用,三角形的中线的性质的运用,三角形三边关系的性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.化简$\sqrt{5×(-2)^{2}}$,结果是 ( )
| A. | 2$\sqrt{5}$ | B. | -2$\sqrt{5}$ | C. | -10 | D. | 10 |
17.下列等式中不一定成立的是( )
| A. | $\frac{y}{x}=\frac{xy}{x^2}$ | B. | $\frac{y}{x}=\frac{πy}{πx}$ | C. | $\frac{y}{x}=\frac{yz}{xz}$ | D. | $\frac{y}{x}=\frac{{y({{x^2}+2})}}{{x({{x^2}+2})}}$ |
18.|a|=a,则有理数a为( )
| A. | 正数 | B. | 负数 | C. | 正数和0 | D. | 负数和0 |
19.三角形的一边长是6,另外两边的长都是方程x2-19x+84=0的根,则该三角形的周长为( )
| A. | 14 | B. | 12 | C. | 12或14 | D. | 25 |
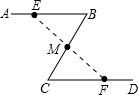 如图、公园里有一条“Z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小石凳E,F,M,且BE=CF,M在BC的中点,试判断三只石凳E,M,F恰好在一直线上吗?为什么?
如图、公园里有一条“Z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小石凳E,F,M,且BE=CF,M在BC的中点,试判断三只石凳E,M,F恰好在一直线上吗?为什么?