题目内容
15.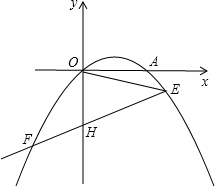 已知抛物线y=-$\frac{1}{3}$x2+$\frac{2}{3}$x经过原点,抛物线与x轴交于另一点A,点E(3,m)在抛物线上,连接OE,作∠OEF=45°,交抛物线于点F,求直线EF的解析式.
已知抛物线y=-$\frac{1}{3}$x2+$\frac{2}{3}$x经过原点,抛物线与x轴交于另一点A,点E(3,m)在抛物线上,连接OE,作∠OEF=45°,交抛物线于点F,求直线EF的解析式.
分析 过点O作OB⊥EF垂足为B,将x=3代入抛物线的解析式求得点E的坐标为(3,-1),由勾股定理求得OE=$\sqrt{10}$,由∠OEF=45°,可知OB=BE=$\sqrt{5}$,设点B的坐标为(x,y),由点之间的距离公式得到关于x、y的方程组,从而可求得点B的坐标,最后利用待定系数法可求得EF的解析式..
解答 解:过点O作OB⊥EF垂足为B.
将x=3代入抛物线的解析式得:y=-1.
∴点E的坐标为(3,-1).
∴OE=$\sqrt{{3}^{2}+(-1)^{2}}$=$\sqrt{10}$.
∵∠OEF=45°,
∴OB=BE=$\sqrt{5}$.
设点B的坐标为(x,y),两点之间的距离公式得:$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=5}\\{(x-3)^{2}+(y+1)^{2}=5}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$,$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$(舍去).
设EF的解析式为y=kx+b.将点B、E的坐标代入直线解解析式得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-2\frac{1}{2}}\end{array}\right.$.
∴直线EF的解析式为y=$\frac{1}{2}x-2\frac{1}{2}$.
点评 本题主要考查的是二次函数的图象和性质、勾股定理、两点之间的距离公式,解二元二次方程组,求得点B的坐标是解题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,求作$\overrightarrow{a}$-$\overrightarrow{b}$.
已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,求作$\overrightarrow{a}$-$\overrightarrow{b}$.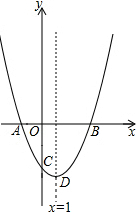 已知二次函数图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点是点D,其中A(-1,0),C(0,-3),对称轴是直线x=1.
已知二次函数图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点是点D,其中A(-1,0),C(0,-3),对称轴是直线x=1.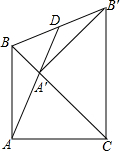 已知,在等腰三角形ABC中,AB=AC,∠BAC=90°,将△ABC绕点C旋转45°成为Rt△CA′B′,连接AA′并延长交BB′于点D,求证:BD=B′D.
已知,在等腰三角形ABC中,AB=AC,∠BAC=90°,将△ABC绕点C旋转45°成为Rt△CA′B′,连接AA′并延长交BB′于点D,求证:BD=B′D.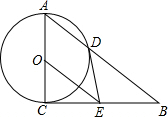 如图,Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点D,OE∥AB交BC于点E,判断DE与⊙O的位置关系,并说明理由.
如图,Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点D,OE∥AB交BC于点E,判断DE与⊙O的位置关系,并说明理由.