题目内容
11.抛物线y=-ax2+bx+2,该抛物线的对称轴为直线x=1且过(-1,0),则抛物线的解析式为y=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2.分析 因为抛物线y=-ax2+bx+2的对称轴为x=-$\frac{b}{2×(-a)}$=1,还经过A(-1,0),所以列方程组即可求得.
解答 解:∵抛物线y=-ax2+bx+2,该抛物线的对称轴为直线x=1且过(-1,0),
$\left\{\begin{array}{l}{-\frac{b}{2×(-a)}=1}\\{-a-b+2=0}\end{array}\right.$
解得:a=$\frac{2}{3}$,b=$\frac{4}{3}$,
∴抛物线的解析式为:y=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2
故答案为:y=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2.
点评 本题考查了用待定系数法求函数解析式的方法,利用代入法解方程组是解答此题的关键,

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
6.若分式$\frac{x-1}{{x}^{2}+1}$的值为零,则x的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | ±1 |
3.估计与$\sqrt{6}$最接近的两个整数是( )
| A. | 2和3 | B. | 4和5 | C. | 5和7 | D. | 35和36 |
20.下列各式能用平方差公式计算的是( )
| A. | (-a+b)(a-b) | B. | (a-b)(a-2b) | C. | (x+1)(x-1) | D. | (-m-n)(m+n) |
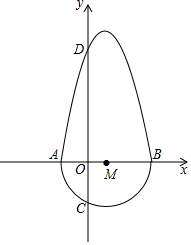 定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为3.
定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为3.
 如图,将一副三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,若∠AOC=70°,则∠BOD的度数为70°.
如图,将一副三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,若∠AOC=70°,则∠BOD的度数为70°.