题目内容
1．若$\left\{\begin{array}{l}{3m+2n=13}\\{2m+n=8}\end{array}\right.$，则m+n=5．分析 求出方程组的解得到m与n的值，代入原式计算即可得到结果．
解答 解：$\left\{\begin{array}{l}{3m+2n=13①}\\{2m+n=8②}\end{array}\right.$，
②×2-①得：m=3，
把m=3代入②得：n=2，
则m+n=3+2=5．
故答案为：5
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
相关题目
12．已知直线y=ax+b（a≠0）经过点A（-3，0）和点B（0，2），那么关于x的方程ax+b=0的解是（ ）
| A． | x=-3 | B． | x=-1 | C． | x=0 | D． | x=2 |
9．下列不能进行平方差计算的是（ ）
| A． | （x+y）（-x-y） | B． | （2a+b）（2a-b） | C． | （-3x-y）（-y+3x） | D． | （a2+b）（a2-b） |
16．下列计算正确的是（ ）
| A． | 2a-a=2 | B． | a2+a=a3 | C． | （x-1）2=x2-1 | D． | （a2）3=a6 |
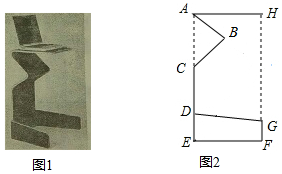如图1是一张创意电脑桌，图2是其平面示意图，已知以A、E、F、H为顶点的四边形，点C、D在AE上，点G在HF上，测得AC=CD=2DE，DE=$\frac{4}{3}$GF，AB=CB=31.2cm，AH=50cm，∠BAH=40°．