题目内容
20.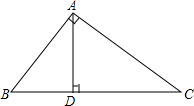 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC.垂足为点D,∠B=60°,AD=3.求BC的长.
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC.垂足为点D,∠B=60°,AD=3.求BC的长.
分析 先由AD⊥BC,垂足为点D,得出∠ADB=∠ADC=90°.在直角△ABD中求出∠BAD=30°,根据30°角所对的直角边等于斜边的一半得出AB=2BD,利用勾股定理得出(2BD)2=BD2+32,求出BD=$\sqrt{3}$;然后在直角△ACD中求出∠C=30°,根据30°角所对的直角边等于斜边的一半得出AC=2AD=6,利用勾股定理得出DC=$\sqrt{A{C}^{2}-A{D}^{2}}$=3$\sqrt{3}$,那么BC=BD+DC=4$\sqrt{3}$.
解答 解:∵AD⊥BC,垂足为点D,
∴∠ADB=∠ADC=90°,
∵∠B=60°,
∴∠BAD=30°,
∴AB=2BD.
∵AB2=BD2+AD2,
∴(2BD)2=BD2+32,
∴BD=$\sqrt{3}$;
∵∠BAC=90°,∠B=60°,
∴∠C=30°,
∴AC=2AD=6,
∴DC=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴BC=BD+DC=$\sqrt{3}$+3$\sqrt{3}$=4$\sqrt{3}$.
点评 本题考查了勾股定理,含30度角的直角三角形的性质,分别求出BD与DC的长是解题的关键.

练习册系列答案
相关题目
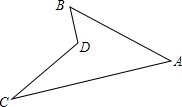 已知如图,求证:∠A+∠B+∠C=∠D.(请思考不同证法)
已知如图,求证:∠A+∠B+∠C=∠D.(请思考不同证法)  如图,∠DAB、∠EBC、∠ACF是△ABC三个不同的外角,则∠DAB+∠EBC+∠ACF=360°.
如图,∠DAB、∠EBC、∠ACF是△ABC三个不同的外角,则∠DAB+∠EBC+∠ACF=360°.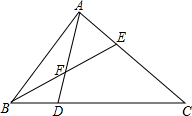 三角形ABC的面积为180,D为BC上最靠近B的4等分点,F为AD上最靠近D的3等分点,那么四边形DCEF的面积是105.
三角形ABC的面积为180,D为BC上最靠近B的4等分点,F为AD上最靠近D的3等分点,那么四边形DCEF的面积是105.