题目内容
甲、乙两个三角形，它们各自三条边的比是2：4：5，甲三角形的最长边是乙三角形最长边的2倍，甲三角形的周长的三分之二比乙三角形的周长多11厘米，问甲乙两个三角形的最短边分别为多少厘米？
考点：相似三角形的判定与性质
专题：常规题型
分析：分别设乙三角形三边分别为2X，4X，5X，根据题干中给出的条件可求出乙三角形的周长，可求出X的值，即可解题．
解答：解：设乙三角形三边为2X，4X，5X，则甲三角形三边分别为4X，8X，10X，
∵甲三角形的周长的三分之二比乙三角形的周长多11厘米，
∴
（4X+8X+10X）=2X+4X+5X+11cm，
解得：X=3cm，
∴乙三角形的最短边为2X=6cm，
甲三角形的最短边为4X=12cm，
∵甲三角形的周长的三分之二比乙三角形的周长多11厘米，
∴
| 2 |
| 3 |
解得：X=3cm，
∴乙三角形的最短边为2X=6cm，
甲三角形的最短边为4X=12cm，
点评：本题考查了相似三角形对应边比例相等的性质，本题中构建方程式求X的值是解题的关键．
练习册系列答案
发散思维新课堂系列答案
相关题目
二次函数y=x2-4x+2与x轴的交点个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
在一块钝角三角形的余料上，加工成正方形零件，使正方形的至少3个顶点都在三角形边上，若三角形的三边长分别为a、b、c，且a＞b＞c，问正方形的2个顶点放在哪条边上可使加工出来的正方形零件面积最大？若|a|+|b|=0，则a、b的关系是（ ）
| A、a=b=0 | B、a=-b |
| C、-a=b | D、a=±b |
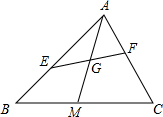如图，在△ABC中，AM是中线，AB=8，AC=6，E、F分别在AB、AC上，且AE=2AF，EF交AM于点G，则
如图，Rt△ABC中，斜边AB上一点M，MN⊥AB交AC于N，若AM=3cm，AB：AC=5：4，求MN的长．