题目内容
19.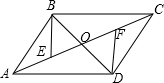 如图,?ABCD的对角线AC、BD相交于点O,AE=CF.
如图,?ABCD的对角线AC、BD相交于点O,AE=CF.(1)求证:△BOE≌△DOF;
(2)若BD=EF,连接DE、BF,判断四边形EBFD的形状,无需说明理由.
分析 (1)先证出OE=OF,再由SAS即可证明△BOE≌△DOF;
(2)由对角线互相平分证出四边形EBFD是平行四边形,再由对角线相等,即可得出四边形EBFD是矩形.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,∴OE=OF,
在△BOE和△DOF中,
$\left\{\begin{array}{l}{OB=OD}&{\;}\\{∠BOE=∠DOF}&{\;}\\{OE=OF}&{\;}\end{array}\right.$,
∴△BOE≌△DOF(SAS);
(2)解:四边形EBFD是矩形;理由如下:
∵OB=OD,OE=OF,
∴四边形EBFD是平行四边形,
∵BD=EF,
∴四边形EBFD是矩形.
点评 本题考查了平行四边形的性质与判定、全等三角形的判定与性质、矩形的判定;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
11.多项式mx2-m与多项式x2-2x+1的公因式是( )
| A. | x-1 | B. | x+1 | C. | x2-1 | D. | (x-1)2 |
 如图,抛物线y=ax2+4与x轴交于A、B两点(A在B的左边),与y轴交于点C,AB=4.
如图,抛物线y=ax2+4与x轴交于A、B两点(A在B的左边),与y轴交于点C,AB=4.
 如图,四边形ABCD是菱形,E、F、G、H分别是各边的中点,随机地向菱形ABCD内掷一粒米,则米粒落到阴影区域内的概率是$\frac{1}{2}$.
如图,四边形ABCD是菱形,E、F、G、H分别是各边的中点,随机地向菱形ABCD内掷一粒米,则米粒落到阴影区域内的概率是$\frac{1}{2}$.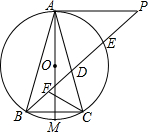 如图,⊙O是△ABC的外接圆,P是⊙O外的一点,AM是⊙O的直径,∠PAC=∠ABC
如图,⊙O是△ABC的外接圆,P是⊙O外的一点,AM是⊙O的直径,∠PAC=∠ABC