题目内容
14. 如图,四边形ABCD是菱形,E、F、G、H分别是各边的中点,随机地向菱形ABCD内掷一粒米,则米粒落到阴影区域内的概率是$\frac{1}{2}$.
如图,四边形ABCD是菱形,E、F、G、H分别是各边的中点,随机地向菱形ABCD内掷一粒米,则米粒落到阴影区域内的概率是$\frac{1}{2}$.
分析 先求出阴影部分的面积与菱形的面积之比,再根据概率公式即可得出答案.
解答 解:∵四边形ABCD是菱形,E、F、G、H分别是各边的中点,
∴四边形HGFE的面积是菱形ABCD面积的$\frac{1}{2}$,
∴米粒落到阴影区域内的概率是$\frac{1}{2}$;
故答案为:$\frac{1}{2}$.
点评 本题考查几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.

练习册系列答案
相关题目
5.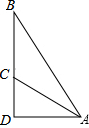 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )| A. | 5米 | B. | 6米 | C. | 8米 | D. | (3+$\sqrt{5}$)米 |
2.某县大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全县学校的设施和设备进行全面改造,2014年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2016年投资7.2亿元人民币,那么每年投资的增长率为( )
| A. | 20% | B. | 40% | C. | -220% | D. | 30% |
6.下列计算正确的是( )
| A. | a2+a2=2a4 | B. | (-a2b)3=-a6b3 | C. | a2•a3=a6 | D. | a8÷a2=a4 |
3.从2,3,4,5中任意选两个数,记作a和b,那么点(a,b)在函数y=$\frac{12}{x}$图象上的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
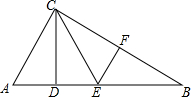 如图所示,在△ABC中,∠ACB=90°,△BEF与△CEF成轴对称,△CEF沿CE翻折与△CED重合,且△ACD≌△EBF.
如图所示,在△ABC中,∠ACB=90°,△BEF与△CEF成轴对称,△CEF沿CE翻折与△CED重合,且△ACD≌△EBF. 如图,已知,在△ABC中,CA=CB,∠ACB=90°,E,F分别是CA,CB边的三等分点,将△ECF绕点C逆时针旋转α角(0°<α<90°),得到△MCN,连接AM,BN.
如图,已知,在△ABC中,CA=CB,∠ACB=90°,E,F分别是CA,CB边的三等分点,将△ECF绕点C逆时针旋转α角(0°<α<90°),得到△MCN,连接AM,BN.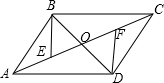 如图,?ABCD的对角线AC、BD相交于点O,AE=CF.
如图,?ABCD的对角线AC、BD相交于点O,AE=CF. 北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)
北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)