题目内容
4.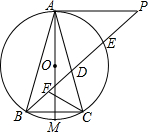 如图,⊙O是△ABC的外接圆,P是⊙O外的一点,AM是⊙O的直径,∠PAC=∠ABC
如图,⊙O是△ABC的外接圆,P是⊙O外的一点,AM是⊙O的直径,∠PAC=∠ABC(1)求证:PA是⊙O的切线;
(2)连接PB与AC交于点D,与⊙O交于点E,F为BD上的一点,若M为$\widehat{BC}$的中点,且∠DCF=∠P,求证:$\frac{BD}{PD}$=$\frac{FD}{ED}$=$\frac{CD}{AD}$.
分析 (1)连接CM,根据圆周角定理得出∠PAC=∠ABC,∠M=∠ABC,得出∠PAC=∠M,由∠M+∠MAC=90°,得出∠PAC+∠MAC=90°,即:∠MAP=90°,就可证得结论;
(2)连接AE,根据垂径定理得出AM⊥BC,进而得出AP∥BC,得出△ADP∽△CDB,根据相似三角形的性质得出$\frac{BD}{PD}$=$\frac{CD}{AD}$,然后证得△ADE∽△CDF,得出$\frac{CD}{DA}$=$\frac{FD}{ED}$,从而证得$\frac{BD}{PD}$=$\frac{FD}{ED}$=$\frac{CD}{AD}$.
解答 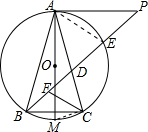 证明:(1)连接CM,
证明:(1)连接CM,
∵∠PAC=∠ABC,∠M=∠ABC,
∴∠PAC=∠M,
∵AM是直径,
∴∠M+∠MAC=90°,
∴∠PAC+∠MAC=90°,
即:∠MAP=90°,
∴MA⊥AP,
∴MA⊥AP,
∴PA是⊙O的切线;
(2)连接AE,
∵M为$\widehat{BC}$中点,AM为⊙O的直径,
∴AM⊥BC,
∵AM⊥AP,
∴AP∥BC,
∴△ADP∽△CDB,
∴$\frac{BD}{PD}$=$\frac{CD}{AD}$,
∵AP∥BC,
∴∠P=∠CBD,
∵∠CBD=∠CAE,
∴∠P=∠DCF,
∴∠DCF=∠CAE,
∵∠ADE=∠CDF,
∴△ADE∽△CDF,
∴$\frac{CD}{DA}$=$\frac{FD}{ED}$,
∴$\frac{BD}{PD}$=$\frac{FD}{ED}$=$\frac{CD}{AD}$.
点评 本题考查了圆周角定理的应用,切线的判定,垂径定理的应用,三角形相似的判定和性质,解答时正确添加辅助线是关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
15.如果一种变换是将抛物线向右平移2个单位或向上平移1个单位,我们把这种变换称为抛物线的简单变换.已知抛物线经过两次简单变换后的一条抛物线是y=x2+1,则原抛物线的解析式不可能的是( )
| A. | y=x2-1 | B. | y=x2+6x+5 | C. | y=x2+4x+4 | D. | y=x2+8x+17 |
12.以下是某手机店1~4月份的统计图,分析统计图,对3、4月份三星手机的销售情况四个同学得出的以下四个结论,其中正确的为( )
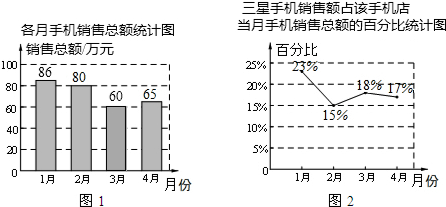

| A. | 4月份三星手机销售额为65万元 | |
| B. | 4月份三星手机销售额比3月份有所上升 | |
| C. | 4月份三星手机销售额比3月份有所下降 | |
| D. | 3月份与4月份的三星手机销售额无法比较,只能比较该店销售总额 |
9.一天晚上,小丽在清洗两只颜色分别为粉色和白色的有盖茶杯时,突然停电了,小丽只好把杯盖和茶杯随机搭配在一起,则其颜色搭配一致的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
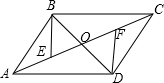 如图,?ABCD的对角线AC、BD相交于点O,AE=CF.
如图,?ABCD的对角线AC、BD相交于点O,AE=CF.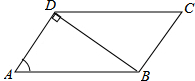 如图,在?ABCD中,连接BD,AD⊥BD,AB=4,sinA=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.
如图,在?ABCD中,连接BD,AD⊥BD,AB=4,sinA=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.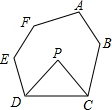 如图,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠DCB,则∠P与∠A+∠B+∠E+∠F的数量关系可表示为∠P=$\frac{1}{2}$(∠A+∠B+∠E+∠F)-180°.
如图,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠DCB,则∠P与∠A+∠B+∠E+∠F的数量关系可表示为∠P=$\frac{1}{2}$(∠A+∠B+∠E+∠F)-180°.