题目内容
2.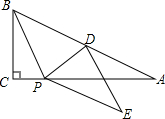 在Rt△ABC中,点D为斜边AB的中点,P为AC边一动点,△BDP沿着PD所在的直线对折,点B的对应点为E.
在Rt△ABC中,点D为斜边AB的中点,P为AC边一动点,△BDP沿着PD所在的直线对折,点B的对应点为E.(1)若BC=5,AC=12,PD⊥AB,求AP的长;
(2)当AD=PE时,求证:四边形BDEP为菱形;
(3)若BC=5,∠A=30°,P点从C点运动到A点,在这个过程中,求E点所经过的路径长.
分析 (1)根据勾股定理求出AB,根据相似三角形的判定定理证明△ADP∽△ACB,根据相似三角形的性质得到比例式,计算即可;
(2)根据四条边相等的四边形是菱形证明即可;
(3)根据等边三角形的性质和平角的定义求出P点从C点运动到A点E点运动的圆心角,根据弧长公式计算即可.
解答 (1)解:∵∠C=90°,BC=5,AC=12,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=13,
∵PD⊥AB,∠C=90°,
∴△ADP∽△ACB,
∴$\frac{AD}{AC}$=$\frac{AP}{AB}$,即$\frac{6.5}{12}$=$\frac{AP}{13}$,
解得,AP=$\frac{169}{24}$;
(2)证明:由翻折变换的性质可知,PB=PE,DB=DE,
∵AD=PE,BD=AD,
∴BP=PE=ED=DB,
∴四边形BDEP为菱形;
(3)∵BC=5,∠A=30°,
∴AB=2BC=10,
∴DE=BD=$\frac{1}{2}$AB=5,
当P点与C点重合时,△BPD是等边三角形,
∴∠BDP=60°,
∴∠EDP=60°,
∴∠EDA=60°,
当P点与A点重合时,∠EDA=180°,
∴P点从C点运动到A点E点运动的圆心角为60°+180°=240°,
$\frac{240×π×5}{180}$=$\frac{20π}{3}$,
∴E点所经过的路径长为$\frac{20π}{3}$.
点评 本题考查的是菱形的判定、弧长的计算、翻折变换的性质,掌握四条边相等的四边形是菱形、弧长的计算公式是解题的关键.

练习册系列答案
相关题目
13.要使函数y=$\sqrt{x-1}$有意义,自变量x的取值范围是( )
| A. | x≥1 | B. | x≤1 | C. | x>1 | D. | x<1 |
10.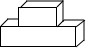 如图,观察这个立体图形,它的俯视图是( )
如图,观察这个立体图形,它的俯视图是( )
 如图,观察这个立体图形,它的俯视图是( )
如图,观察这个立体图形,它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
12. 我国宣布划设东海防空识别区如图所示,具体范围为六点连线与我领海线之间空域.其A、B、C三点的坐标数据如表:
我国宣布划设东海防空识别区如图所示,具体范围为六点连线与我领海线之间空域.其A、B、C三点的坐标数据如表:
(1)A点与B或C两点的经度差为$\frac{10}{3}$(单位:度).
(2)通过测量发现,∠BAC=95°,∠BCA=30°,已知北纬31°00′(即点A所在的纬度)处两条相差1°的经线之间的实际距离为96km.我空军一架巡逻机在该区域执行巡逻任务,飞行速度为30km/min,求飞机沿东经125°经线方向从B点飞往C点大约需要多少时间.(已知tan35°=0.7,tan55°=$\frac{10}{7}$,结果保留整数)
 我国宣布划设东海防空识别区如图所示,具体范围为六点连线与我领海线之间空域.其A、B、C三点的坐标数据如表:
我国宣布划设东海防空识别区如图所示,具体范围为六点连线与我领海线之间空域.其A、B、C三点的坐标数据如表:| A | B | C | |
| 北纬(度) | 31°00′ | 33°11′ | 25°38′ |
| 东经(度) | 128°20′ | 125°00′ | 125°00′ |
(2)通过测量发现,∠BAC=95°,∠BCA=30°,已知北纬31°00′(即点A所在的纬度)处两条相差1°的经线之间的实际距离为96km.我空军一架巡逻机在该区域执行巡逻任务,飞行速度为30km/min,求飞机沿东经125°经线方向从B点飞往C点大约需要多少时间.(已知tan35°=0.7,tan55°=$\frac{10}{7}$,结果保留整数)
 甲乙两人玩纸牌游戏,如图是同一副扑克中的4张扑克牌的正面,将它们正面朝下后放在桌上,甲先从中抽出一张,乙从剩余的3张牌中也抽出一张.
甲乙两人玩纸牌游戏,如图是同一副扑克中的4张扑克牌的正面,将它们正面朝下后放在桌上,甲先从中抽出一张,乙从剩余的3张牌中也抽出一张.