题目内容
 已知在⊙O上,A、B分别为
已知在⊙O上,A、B分别为 |
| CD |
 |
| EF |
考点:圆心角、弧、弦的关系
专题:证明题
分析:先根据A、B分别为
,
的中点得出
=
,
=
,再根据AM=BN可知
=
,故可得出
=
,由此可得出结论.
 |
| CD |
 |
| EF |
 |
| AD |
| 1 |
| 2 |
 |
| CD |
 |
| BE |
| 1 |
| 2 |
 |
| EF |
 |
| AD |
 |
| BE |
 |
| CD |
 |
| EF |
解答:证明:∵A、B分别为
,
的中点,
∴
=
,
=
,
∵AM=BN,
∴
=
,
∴
=
,
∴CD=EF.
 |
| CD |
 |
| EF |
∴
 |
| AD |
| 1 |
| 2 |
 |
| CD |
 |
| BE |
| 1 |
| 2 |
 |
| EF |
∵AM=BN,
∴
 |
| AD |
 |
| BE |
∴
 |
| CD |
 |
| EF |
∴CD=EF.
点评:本题考查的是圆心角、弧、弦的关系,熟知在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等是解答此题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知y=kx+b,当x=0时,y=2;当x=2时,y=0,则当x=-2时,y等于( )
| A、-2 | B、0 | C、2 | D、4 |
 如图所示平面直角坐标系中,矩形OABC的顶点B的坐标为(4,8),若一次函数y=kx+2的图象平分矩形OABC的面积.
如图所示平面直角坐标系中,矩形OABC的顶点B的坐标为(4,8),若一次函数y=kx+2的图象平分矩形OABC的面积.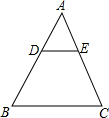 如图,△ABC中,已知,DE∥BC,AD=
如图,△ABC中,已知,DE∥BC,AD=
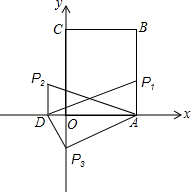
 如图,某校7年级的学生从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8km到A处,又往正南方向走4km到B处,又折向正东方向走6km到C处,再折向正北方向走8km到D处,最后又往正东方向走4km才到探险地P;取点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2km为一个单位长度建立平面直角坐标系.
如图,某校7年级的学生从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8km到A处,又往正南方向走4km到B处,又折向正东方向走6km到C处,再折向正北方向走8km到D处,最后又往正东方向走4km才到探险地P;取点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2km为一个单位长度建立平面直角坐标系.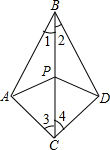 如图在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是BC上任意一点.求证:PA=PD.
如图在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是BC上任意一点.求证:PA=PD.