题目内容
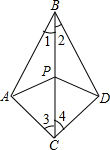 如图在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是BC上任意一点.求证:PA=PD.
如图在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是BC上任意一点.求证:PA=PD.考点:全等三角形的判定与性质,线段垂直平分线的性质
专题:证明题
分析:由已知两对角相等,且夹边为公共边相等,利用ASA得到△ABC≌△DBC,利用全等三角形对应边相等得到AB=DB,再利用SAS得到△ABP≌△DBP,利用全等三角形对应边相等即可得证.
解答:证明:在△ABC和△DBC中,
,
∴△ABC≌△DBC(ASA),
∴AB=DB,
在△ABP和△DBP中,
,
∴△ABP≌△DBP(SAS),
∴AP=DP.
|
∴△ABC≌△DBC(ASA),
∴AB=DB,
在△ABP和△DBP中,
|
∴△ABP≌△DBP(SAS),
∴AP=DP.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
下列各组数不是互为倒数的是( )
| A、-1与-1 | ||||
B、2.5与
| ||||
C、2或-
| ||||
D、-
|
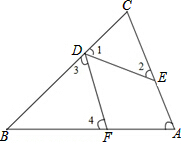 如图,在△ABC,∠A=70°,D、E、F分别在BC、AC、AB上,且∠1=∠2,∠3=∠4,则∠EDF等于( )
如图,在△ABC,∠A=70°,D、E、F分别在BC、AC、AB上,且∠1=∠2,∠3=∠4,则∠EDF等于( )| A、70° | B、65° |
| C、55° | D、45° |
 已知在⊙O上,A、B分别为
已知在⊙O上,A、B分别为
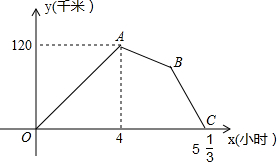 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用50分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用50分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论: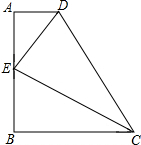 如图在四边形ABCD中,∠A=∠B=90°,CE平分∠BCD,AE=BE.求证:
如图在四边形ABCD中,∠A=∠B=90°,CE平分∠BCD,AE=BE.求证: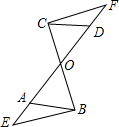 如图,AB∥CD,OA=OD,点F、D、O、A、E在同一直线上,AE=DF,求证:EB∥CF.
如图,AB∥CD,OA=OD,点F、D、O、A、E在同一直线上,AE=DF,求证:EB∥CF.