题目内容
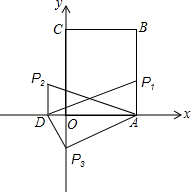 如图所示平面直角坐标系中,矩形OABC的顶点B的坐标为(4,8),若一次函数y=kx+2的图象平分矩形OABC的面积.
如图所示平面直角坐标系中,矩形OABC的顶点B的坐标为(4,8),若一次函数y=kx+2的图象平分矩形OABC的面积.(1)求一次函数的解析式.
(2)求(1)中一次函数与矩形的交点坐标.
(3)设点D(-1,0),在一次函数图象上求一点P,使△ADP为直角三角形,求点P坐标.
考点:一次函数综合题
专题:压轴题
分析:(1)求出矩形的中心坐标,再根据矩形的性质,过矩形中心的直线把矩形分成面积相等的两部分,然后代入计算即可得解;
(2)令x=0,x=4,利用一次函数解析式求解即可;
(3)分点D是直角顶点,点A是直角顶点,利用一次函数解析式计算即可;点P是直角顶点,设点P(a,a+2),过点P作PE⊥x轴于E,根据△APE和△PDE相似,利用相似三角形对应边成比例列式计算即可得解.
(2)令x=0,x=4,利用一次函数解析式求解即可;
(3)分点D是直角顶点,点A是直角顶点,利用一次函数解析式计算即可;点P是直角顶点,设点P(a,a+2),过点P作PE⊥x轴于E,根据△APE和△PDE相似,利用相似三角形对应边成比例列式计算即可得解.
解答:解:(1)∵点B的坐标为(4,8),
∴矩形OABC的中心坐标为(2,4),
∵一次函数y=kx+2的图象平分矩形OABC的面积,
∴2k+2=4,
解得k=1,
所以,一次函数的解析式为y=x+2;
(2)x=0时,y=2,
x=4时,y=4+2=6,
所以,一次函数与矩形的交点坐标为(0,2),(4,6);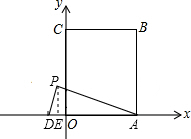
(3)若点D是直角顶点,则x=-1时,y=-1+2=1,
点P的坐标为(-1,1),
若点A是直角顶点,则x=4,y=4+2=6,
点P的坐标为(4,6),
若P是直角顶点,设点P(a,a+2),
过点P作PE⊥x轴于E,则△APE∽△PDE,
所以,
=
,
所以,
=
,
整理得,2a2+a=0,
解得a1=0,a2=-
,
当a=0时,a+2=2,
当a=-
时,a+2=
,
所以,点P的坐标为(0,2)或(-
,
);
综上所述,△ADP为直角三角形时,点P的坐标为(-1,1)或(4,6)或(0,2)或(-
,
).
∴矩形OABC的中心坐标为(2,4),
∵一次函数y=kx+2的图象平分矩形OABC的面积,
∴2k+2=4,
解得k=1,
所以,一次函数的解析式为y=x+2;
(2)x=0时,y=2,
x=4时,y=4+2=6,
所以,一次函数与矩形的交点坐标为(0,2),(4,6);

(3)若点D是直角顶点,则x=-1时,y=-1+2=1,
点P的坐标为(-1,1),
若点A是直角顶点,则x=4,y=4+2=6,
点P的坐标为(4,6),
若P是直角顶点,设点P(a,a+2),
过点P作PE⊥x轴于E,则△APE∽△PDE,
所以,
| AE |
| PE |
| PE |
| DE |
所以,
| 4-a |
| a+2 |
| a+2 |
| a-(-1) |
整理得,2a2+a=0,
解得a1=0,a2=-
| 1 |
| 2 |
当a=0时,a+2=2,
当a=-
| 1 |
| 2 |
| 3 |
| 2 |
所以,点P的坐标为(0,2)或(-
| 1 |
| 2 |
| 3 |
| 2 |
综上所述,△ADP为直角三角形时,点P的坐标为(-1,1)或(4,6)或(0,2)或(-
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题是一次函数综合题型,主要利用了矩形的性质,待定系数法求一次函数解析式,一次函数图象上点的坐标特征,相似三角形的判定与性质,难点在于(1)熟记过矩形中心的直线把矩形分成面积相等的两部分,(3)分情况讨论.

练习册系列答案
相关题目
下列方程的变形中,正确的是( )
| A、由2=3-x,得x=2+3 | ||||
| B、由6y=4,得y=4-6 | ||||
C、由
| ||||
| D、由4-x=2x,得2x-x=4 |
 一辆园林喷灌车和一辆公交车分别从一条笔直公路两端点A、B同时出发匀速行驶,喷灌车中途停车在供水站加满水后继续以原速进行作业到达终点B,公交车到达A处进站检修,之后沿原路原点返回到点B.如图是两车与点A的距离y(千米)与运行时间t(时)的函数图象.
一辆园林喷灌车和一辆公交车分别从一条笔直公路两端点A、B同时出发匀速行驶,喷灌车中途停车在供水站加满水后继续以原速进行作业到达终点B,公交车到达A处进站检修,之后沿原路原点返回到点B.如图是两车与点A的距离y(千米)与运行时间t(时)的函数图象.
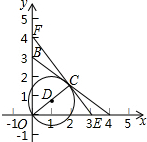 如图,在平面直角坐标系中,点A、B的坐标分别为(a,0),(0,b),且a:b=4:3,点C是AB的中点,以OC为直径作圆D,且圆D的直径为
如图,在平面直角坐标系中,点A、B的坐标分别为(a,0),(0,b),且a:b=4:3,点C是AB的中点,以OC为直径作圆D,且圆D的直径为 如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,交AB于点D.
如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,交AB于点D. 已知在⊙O上,A、B分别为
已知在⊙O上,A、B分别为
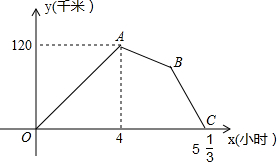 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用50分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用50分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论: