题目内容
13. 如图,梯形ABCD中,AB∥CD,∠B=∠C=90°,点F在BC边上,AB=8,CD=2,BC=10,若△ABF与△FCD相似,则CF的长为2或8.
如图,梯形ABCD中,AB∥CD,∠B=∠C=90°,点F在BC边上,AB=8,CD=2,BC=10,若△ABF与△FCD相似,则CF的长为2或8.
分析 分△ABF∽△FCD和△ABF∽△DCF两种情况,根据相似三角形的性质解答即可.
解答 解:当△ABF∽△FCD时,
$\frac{AB}{CF}$=$\frac{BF}{CD}$,即$\frac{8}{CF}$=$\frac{10-CF}{2}$,
解得,CF=8;
当△ABF∽△DCF时,
$\frac{AB}{CD}$=$\frac{BF}{CF}$,即$\frac{8}{2}$=$\frac{10-CF}{CF}$,
解得,CF=2,
故答案为:2或8.
点评 本题考查的是相似三角形的性质,掌握相似三角形的对应边的比相等是解题的关键,注意分情况讨论思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.下列方程,是一元二次方程的是( )
| A. | x2+3x-1=0 | B. | y2-5x=1 | C. | 2x+1=0 | D. | $\frac{1}{x}$+x2=1 |
5.下列计算正确的是( )
| A. | a3•a2=a6 | B. | (-a2)3=a6 | C. | a3+a4=a7 | D. | a2•(a3)4=a14 |
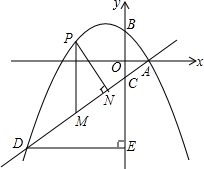 如图,抛物线y=-$\frac{1}{4}$x2+bx+c与x轴交于点A(2,0),交y轴于点B(0,$\frac{5}{2}$)直线y=kx-$\frac{3}{2}$过点A与y轴交于点C与抛物线的另一个交点是D.
如图,抛物线y=-$\frac{1}{4}$x2+bx+c与x轴交于点A(2,0),交y轴于点B(0,$\frac{5}{2}$)直线y=kx-$\frac{3}{2}$过点A与y轴交于点C与抛物线的另一个交点是D.