题目内容
4.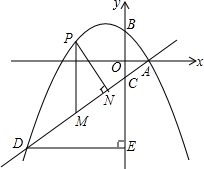 如图,抛物线y=-$\frac{1}{4}$x2+bx+c与x轴交于点A(2,0),交y轴于点B(0,$\frac{5}{2}$)直线y=kx-$\frac{3}{2}$过点A与y轴交于点C与抛物线的另一个交点是D.
如图,抛物线y=-$\frac{1}{4}$x2+bx+c与x轴交于点A(2,0),交y轴于点B(0,$\frac{5}{2}$)直线y=kx-$\frac{3}{2}$过点A与y轴交于点C与抛物线的另一个交点是D.(1)求抛物线y=-$\frac{1}{4}$x2+bx+c与直线y=kx-$\frac{3}{2}$的解析式;
(2)设点P是直线AD上方的抛物线上一动点(不与点A、D重合),过点P作y轴的平行线,交直线AD于点M,作DE⊥y轴于点E.探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在请求出点P的坐标;若不存在,请说明理由;
(3)在(2)的条件下,作PN⊥AD于点N,设△PMN的周长为L,点P的横坐标为x,求L与x的函数关系式,并求出L的最大值.
分析 (1)将A,B两点分别代入y=$\frac{1}{4}$x2+bx+c进而求出解析式即可;
(2)首先假设出P,M点的坐标,进而得出PM的长,将两函数联立得出D点坐标,进而得出CE的长,利用平行四边形的性质得出PM=CE,得出等式方程求出即可;
(3)利用勾股定理得出DC的长,进而根据△PMN∽△CDE,得出两三角形周长之比,求出l与x的函数关系,再利用配方法求出二次函数最值即可.
解答  解:(1)∵y=-$\frac{1}{4}$x2+bx+c经过点A(2,0)和B(0,$\frac{5}{2}$),
解:(1)∵y=-$\frac{1}{4}$x2+bx+c经过点A(2,0)和B(0,$\frac{5}{2}$),
∴由此得 $\left\{\begin{array}{l}{-1+2b+c=0}\\{c=\frac{5}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-\frac{3}{4}}\\{c=\frac{5}{2}}\end{array}\right.$.
∴抛物线的解析式是y=-$\frac{1}{4}$x2-$\frac{3}{4}$x+$\frac{5}{2}$,
∵直线y=kx-$\frac{3}{2}$经过点A(2,0)
∴2k-$\frac{3}{2}$=0,
解得:k=$\frac{3}{4}$,
∴直线的解析式是y=$\frac{3}{4}$x-$\frac{3}{2}$,
(2)设P的坐标是(x,-$\frac{1}{4}$x2-$\frac{3}{4}$x+$\frac{5}{2}$),则M的坐标是(x,$\frac{3}{4}$x-$\frac{3}{2}$)
∴PM=(-$\frac{1}{4}$x2-$\frac{3}{4}$x+$\frac{5}{2}$)-($\frac{3}{4}$x-$\frac{3}{2}$)=-$\frac{1}{4}$x2-$\frac{3}{2}$x+4,
解方程 $\left\{\begin{array}{l}{y=-\frac{1}{4}{x}^{2}-\frac{3}{4}x+\frac{5}{2}}\\{y=\frac{3}{4}x+\frac{5}{2}}\end{array}\right.$得:$\left\{\begin{array}{l}{x=-8}\\{y=-7\frac{1}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$,
∵点D在第三象限,则点D的坐标是(-8,-7$\frac{1}{2}$),由y=$\frac{3}{4}$x-$\frac{3}{2}$得点C的坐标是(0,-$\frac{3}{2}$),
∴CE=-$\frac{3}{2}$-(-7$\frac{1}{2}$)=6,
由于PM∥y轴,要使四边形PMEC是平行四边形,必有PM=CE,即-$\frac{1}{4}$x2-$\frac{3}{2}$x+4=6
解这个方程得:x1=-2,x2=-4,
符合-8<x<2,
当x=-2时,y=-$\frac{1}{4}$×(-2)2-$\frac{3}{4}$×(-2)+$\frac{5}{2}$=3,
当x=-4时,y=-$\frac{1}{4}$×(-4)2-$\frac{3}{4}$×(-4)+$\frac{5}{2}$=$\frac{3}{2}$,
因此,直线AD上方的抛物线上存在这样的点P,使四边形PMEC是平行四边形,点P的坐标是(-2,3)和(-4,$\frac{3}{2}$);
(3)在Rt△CDE中,DE=8,CE=6 由勾股定理得:DC=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∴△CDE的周长是24,
∵PM∥y轴,
∵∠PMN=∠DCE,
∵∠PNM=∠DEC,
∴△PMN∽△CDE,
∴$\frac{{△}_{PMN}的周长}{{△}_{CDE}的周长}$=$\frac{PM}{DC}$,即$\frac{l}{24}$=$\frac{-\frac{1}{4}{x}^{2}-\frac{3}{2}x+4}{10}$,
化简整理得:l与x的函数关系式是:l=-$\frac{3}{5}$x2-$\frac{18}{5}$x+$\frac{48}{5}$,
l=-$\frac{3}{5}$x2-$\frac{18}{5}$x+$\frac{48}{5}$=-$\frac{3}{5}$(x+3)2+25,
∵-$\frac{3}{5}$<0,
∴l有最大值,
当x=-3时,l的最大值是25.
点评 此题主要考查了二次函数的最值求法以及待定系数法求二次函数解析式和函数交点求法以及平行四边形的性质等知识,利用数形结合得出PM=CE进而得出等式是解题关键.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案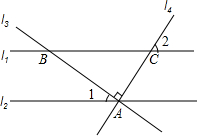 如图,已知直线l1∥l2,直线l3⊥l4于A,在l2上,若∠1=27°,则∠2的度数为( )
如图,已知直线l1∥l2,直线l3⊥l4于A,在l2上,若∠1=27°,则∠2的度数为( )| A. | 27° | B. | 53° | C. | 63° | D. | 54° |
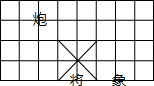 若在象棋盘上建立直角坐标系,使“将”位于点(1,-1),“象”位于点(3,-1),则“炮”位于点( )
若在象棋盘上建立直角坐标系,使“将”位于点(1,-1),“象”位于点(3,-1),则“炮”位于点( )| A. | (1,3) | B. | (-1,1) | C. | (-1,2) | D. | (-1,3) |
| A. | x2+2x=x2-1 | B. | $\frac{1}{x}$-1=2x2=0 | C. | ax2+bx+c=0 | D. | (x+1)2=2(x+1) |

| A. | 3a1+4a2+3a3 | B. | 3a1+3a2+3a3 | C. | 4a1+3a2+4a3 | D. | 4a1+4a2+4a3 |
| A. | 1 | B. | -1 | C. | 6 | D. | -6 |
 如图,梯形ABCD中,AB∥CD,∠B=∠C=90°,点F在BC边上,AB=8,CD=2,BC=10,若△ABF与△FCD相似,则CF的长为2或8.
如图,梯形ABCD中,AB∥CD,∠B=∠C=90°,点F在BC边上,AB=8,CD=2,BC=10,若△ABF与△FCD相似,则CF的长为2或8.