题目内容
观察图形：将一张长方形纸片对折，可得到一条折痕．继续对折，对折是每次折痕与上次折痕保持平行，那么对折8次后折痕的条数是（ ）
| A、16 | B、64 |
| C、128 | D、255 |
考点：规律型：图形的变化类
专题：
分析：观察图形并结合折痕的条数可得，折痕的条数加上1后成2的指数次幂变化，根据此规律找出第n次对折后的折痕的条数表达式，然后把n=8代入进行计算即可得解．
解答：解：对折1次，折痕为1条，1=21-1，
对折2次，折痕为3条，3=22-1，
对折3次，折痕为7条，7=23-1，
…，
依此类推，对折n次，折痕为2n-1条，
所以，当n=8时，28-1=255．
故选D．
对折2次，折痕为3条，3=22-1，
对折3次，折痕为7条，7=23-1，
…，
依此类推，对折n次，折痕为2n-1条，
所以，当n=8时，28-1=255．
故选D．
点评：本题是对图形变化规律的考查，根据数据的特点，发现与2的指数次幂相接近，从而得到变化规律是解题的关键．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
如图，足球由正五边形和正六边形皮块缝成，试用正六边形的块数x表示正五边形的块数y，并指出其中的变量和常量．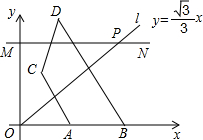
如图，长度为2的动线段AB在x轴上向右移动，设A（x，0），其中x＞0，线段AB关于射线l：y=
如图，C在直线BE上，∠ABC与∠ACE的角平分线交于点A1．